DeepLearning

一、基础知识

安装环境

conda create -n -y d2l python=3.8
conda activate d2l
pip install -y jupyter d2l torch torchvision rise
wget https://zh-v2.d2l.ai/d2l-zh.zip
unzip -d d2l d2l-zh.zip

1.1 Pytorch 中的梯度计算图

在 Pytorch 中自动维护了张量的计算图，用于计算梯度。其中有三种节点，分别是：

• 叶子节点
• 中间节点
• 输出节点

顾名思义，叶子节点就是最原始的输入变量。例如有如下计算过程：

a = torch.tensor([2.], requires_grad=True)  
b = a ** 2  
c = b + 1

a 变量就是叶子节点，然后我们在 c 张量上执行反向传播算法：

c.backward()  
a.grad
# tensor([4.])

可以看到成功输出了梯度。值得注意的是，梯度只能存在于叶子节点中，而不能存在于中间变量中。

此外，中间节点也可以进行反向传播，但是与输出节点反向传播相比，叶子节点的梯度可能不同，归根到底是梯度计算图的路径不同。

例如：

a = torch.tensor([2.], requires_grad=True)  
b = a ** 2  
c = b ** 2  
b.backward()  
a.grad
# tensor([4.])

上面是从中间节点反向传播，梯度为 4。

a = torch.tensor([2.], requires_grad=True)  
b = a ** 2  
c = b ** 2  
c.backward()  
a.grad
# tensor([32.])

上面是从输出节点反向传播，梯度则为 32。

在一些情况下，我们可能希望计算图并不记录运算过程，例如在推理阶段。使用如下的代码即可做到。

a = torch.tensor([2.], requires_grad=True)  
with torch.no_grad():  
    b = a ** 2

此外，还有另外一种做法：

a = torch.tensor([2.], requires_grad=True)  
a1 = a.detach()  
b = a1 ** 2  
b.requires_grad
# False

.detach() 方法可以创建一个相同但是不可导的张量，从而阻断计算图的追踪。

与 .detach() 相似的是 .detach_() ，.detach_() 对变量本身进行更改，并不创建新的张量。

具体来说，.detach_() 做两件事情：

• 设置 grad_fn 为 None，这样就切断了之前的节点。
• 设置 require_grad 为 False，这样当后面的节点进行反向传播时就会将其看做普通标量。

a = torch.tensor([2.], requires_grad=True)  
b2 = torch.tensor([3.], requires_grad=True)  
b = a ** 2  
b.detach_()  
c = b * b2  
c.backward()  
print(b2.grad)
# tensor([4.])

可以看到，b2 的梯度实际上就是 b。

对于一个张量，比如 a，若 a-->b 存在，且 a-->c 存在，则 b 与 c 进行反向传播之后，张量 a 的梯度会累加，举例如下。

a = torch.tensor([2.], requires_grad=True)  
b = a ** 2  
c = a ** 3  
b.backward()  
print(a.grad)  
c.backward()  
print(a.grad)
# tensor([4.])
# tensor([16.])

可以看到，张量 c 在反向传播后，梯度其实应该是 12，但是却变成了 16。

参考：

https://www.bilibili.com/video/BV1LL41147G8?t=1.8

二、线性神经网络

2.1 线性回归

2.1.1 基础知识

线性模型有一个 n 维的权重和一个标量偏移，输出是输入的加权和，即

衡量预测值好坏：

由于有权重的只有一层，因此线性回归可以看作是单层神经网络。

2.1.2 基础优化算法

梯度下降算法：

但是如果数据集规模太大，整体计算一遍才能进行一次优化过程，效率很低，因此就诞生了小批量梯度下降。即从整体数据中取出一个小批量 mini-batch，然后在这个小批量上计算梯度。

设一个 mini-batch 的样本数为 b, 则损失为：

2.2 Softmax回归

2.2.1 基础知识

Softmax实际是分类问题

独热编码：

将预测值转换为概率

exp是为了让负数转换为正数

如何衡量两个概率的区别呢？-->交叉熵

则损失函数如下，可以看出只关心真实类别对应的概率

2.2.2 损失函数

L2Loss：均方损失

L1Loss：绝对值损失

Huber's Robust Loss

四、多层感知机

4.1 感知机

等价于批量大小为 1 的梯度下降，并使用如下的损失函数:

感知机有什么问题：感知机只能产生线性分割面

小结:

1. 感知机是一个二分类模型，是最早的AI模型之一
2. 求解算法等价于使用批量大小为1的梯度下降
3. 不能拟合XOR 函数

4.2 多层感知机

mlp

为什么需要激活函数:

可以看到,最终的效果是和单层感知机相同的,因此需要加入非线性的激活函数,也就是

Sigmoid激活函数:

sigmoid

Tanh激活函数:

tanh

ReLu激活函数:

relu

4.3 模型选择

训练误差: 模型在训练数据上的误差

泛化误差：模型在新数据上的误差

验证数据集：一个用来评估模型好坏的数据集

测试数据集: 只用一次的数据集，比如未来才会得到的数据集

若数据不多，则可以使用K-折交叉验证的方法：将训练数据分为k块，对于i从0到k-1，每次取第i块为验证数据集，其余为训练数据集，误差取k个验证集的平均，通常k=5或10

4.4 过拟合和欠拟合

模型容量	简单	复杂
低	正常	欠拟合
高	过拟合	正常

过拟合欠拟合

可以看到当模型复杂度过高，模型会过于关注一些无关紧要的噪声

那么如何估计模型容量呢？

• 在不同种类的算法之间，比如树模型和神经网络，难以比较
• 但如果给定了一个模型种类，将有两个主要因素
  1. 参数的个数
  2. 参数值的选择范围

数据复杂度:

• 样本个数
• 每个样本的元素个数
• 时间、空间结构
• 多样性

4.5 权重衰退

定义：是用来处理过拟合的一种方法

1. 使用均方范数作为硬性限制:

通过限制参数值的选择范围来控制模型容量：

通常不会限制 b

2. 使用均方范数作为柔性限制:

对于每个，都可以找到使得之前的目标函数等价于下面

若 ，则 ；若 ，则无作用。

通常

实现：

self.optimizer = torch.optim.SGD([
            {
                "params": self.model[0].weight,
                "weight_decay": 1e-3
            },
            {
                "params": self.model[0].bias,
            },
        ], lr=0.01)

4.6 丢弃法

丢弃法也是解决过拟合的有效方法之一

丢弃法对每个元素进行如下扰动：

正则项只在训练中使用，但在推理过程中不使用，这样能保证确定的输出

4.7 数值稳定性

梯度爆炸的问题：

• 值超过值域
• 对学习率敏感：我们可能需要在训练过程中不断调整学习率

梯度消失的问题：

• 梯度值变成0
• 训练没有进展
• 无法让神经网络更深

如何让训练更加稳定：

• 将乘法变加法
• 梯度归一化
• 梯度裁剪
• 合理的权重初始化和激活函数

在训练刚开始的时候更容易有数值不稳定。因此，如何初始化才能让数值比较稳定呢？

下面讲解 Xavier 初始化。

对于i层神经元的输出，有

因此有

同理,对于反向传播

因此

因此有正态分布初始化

均匀分布初始化

上面的公式需要假设

1. ,
2. 激活函数对称且
3. X 的方差相同

参考：

• https://www.bilibili.com/video/BV1tq4y1K7Kk?t=709.7
• https://www.bilibili.com/video/BV1PF411K7nb?t=2.1

五、卷积神经网络

5.1 卷积层

no_padding_no_strides|294

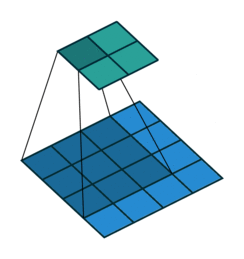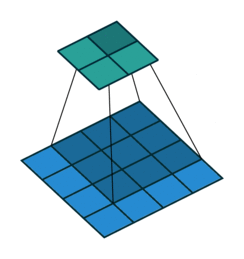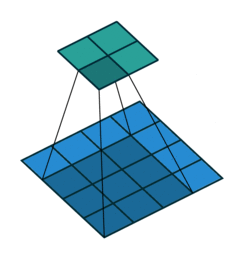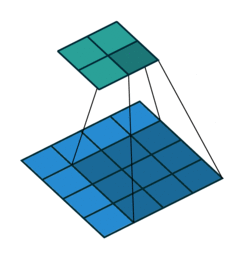
输入X：

核W：

输出Y：

5.2 填充和步幅

为什么需要填充？卷积核可以减小输出大小。

arbitrary_padding_no_strides_transposed|320

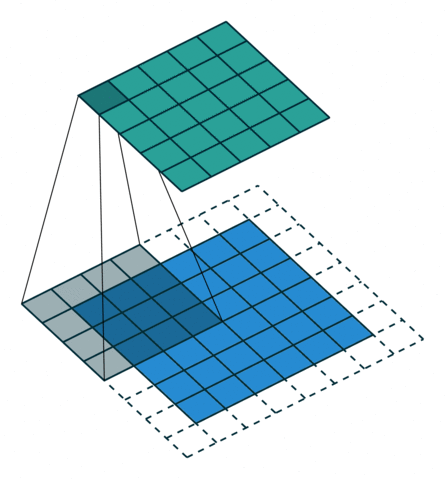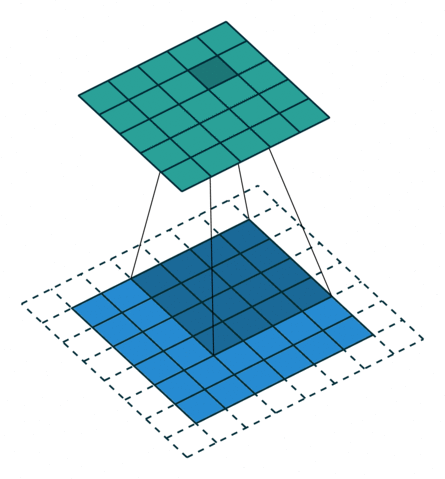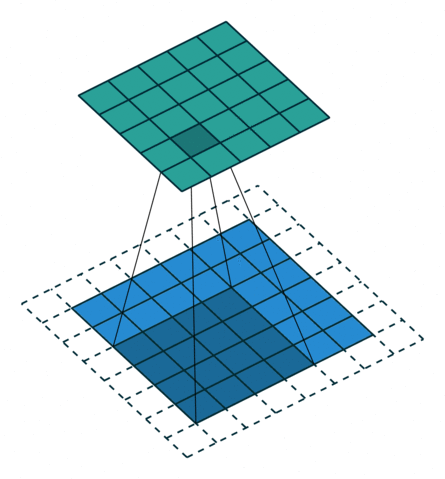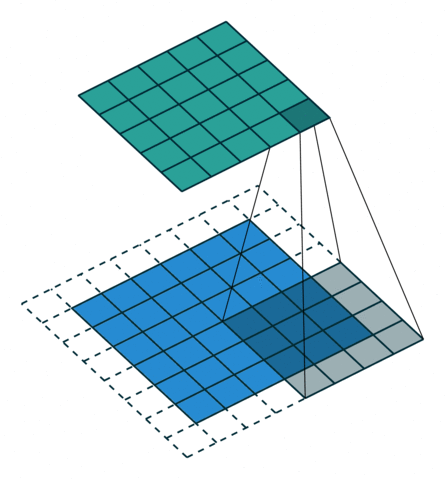
假设填充行和列，则输出形状为：

通常取

• 当为奇数，上下各填充
• 当为偶数，上侧填充,下侧填充

步幅的作用：加快减小输出的大小

no_padding_strides|344

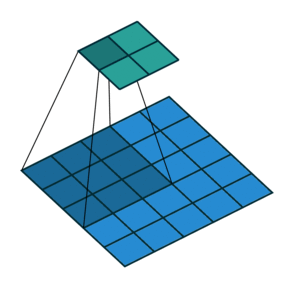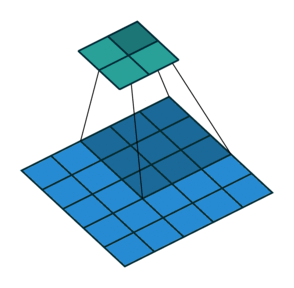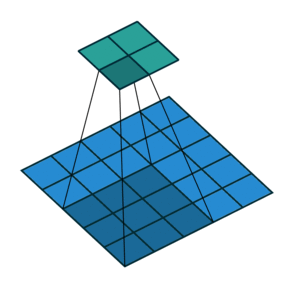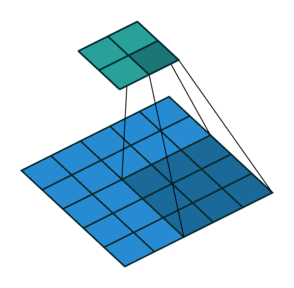
5.3 多输入输出通道

如果有多个输入通道，比如RGB有3个通道，则每个通道都有一个卷积核，结果是所有通道卷积结果的和。

多输出通道：可以有多个三维卷积核

5.4 池化层

池化层用来降低后续层的输入维度，缩减模型大小，提高计算速度，防止过拟合。

主要分为两种：

• 最大池化
• 平均池化

5.5 LeNet

LeNet 在 1989 年提出，是最早提出的卷积神经网络之一，先使用卷积层学习图片的空间信息，然后使用全连接层转换到类别空间。

从图中可以看到，LeNet 主要分成两部分，一个是卷积层，一个是全连接层。在卷积层，首先经过一个 6 通道的卷积，再经过一个池化层；然后经过 16 通道的卷积，最后通过一个池化层；然后就进入全连接层进行分类。

5.6 AlexNet

AlexNet 在 2012 年被提出，可以看做是更深更大的 LeNet。

|358|333

上图中左侧为 LeNet，右侧为 AlexNet。

改进点：

• 新增了 Dropout
• 激活函数从Sigmoid 变为 ReLu
• 池化层从平均池化变为最大池化

5.7 使用块的网络VGG

AlexNet 的效果很好，但是很多层设计的过于随意。为了设计新的网络，有没有办法寻找一种模板呢？这就引出了 VGG。

|325

从图中可以看出，VGG 可以看做是对 AlexNet 的一种抽象和封装，使之更加模块化。在一个 VGG 块中，首先是 n 层的 3*3 卷积，pad 为 1，然后是一个 2*2 的最大池化层。值得注意的是，VGG 的提出者也曾使用了 5*5 的卷积，但是他们发现，更小的卷积核+更多的层数往往效果比更大的卷积核+更少的层数好。

5.8 网络中的网络 NiN

无论是 AlexNet 还是 VGG，都有全连接层的存在。这样有两个缺点存在。一个是全连接层的参数数目过多，训练过于昂贵。另外就是使用全连接层可能会完全放弃表征的空间结构。因此 NiN 被提出，放弃了全连接层而全部使用卷积层。

|400

从图中可以看出，一个 NiN 块由 3 部分组成，分别是一个卷积层和两个 1*1 的卷积层。实际上可以看做是另一种形式的全连接。几个 1*1 的卷积层可以用来融合通道。最后，通过全局平均汇聚层获取输出结果。

5.9 GoogLeNet

GoogLeNet 吸收了 NiN 中 1*1 卷积的思想，在此基础上进行了改进。在之前的网络中，总是纠结于选择什么样的卷积核。然而 GoogLeNet 告诉我们，可以全部选择，并行计算。

例如，下面是一个 Inception-v1 块：

最终的输入和输出的高宽是相同的，不同的只是通道数。前面 3 条路径分别从不同大小的卷积核上提取信息。中间的两条 1*1 卷积用于降低通道数，从而减小模型复杂性。最后一条路径也是用来改变通道数。在 Inception 块中，我们通常需要调整的超参是每层的输出通道数。

|198

上图就是 GoogLeNet 的网络架构，使用了不同的 Inception 块。

后来的研究者对 Inception 块进行了不同程度的改进，诞生了 Inception-v2 (添加了 batch-normalization)，Inception-v3 (替换一些卷积层)，Inception-v4 (使用残差连接)。

5.10 批量归一化

为什么需要进行批量归一化？距离来说，对于一个比较深层的网络，越接近输出层的位置梯度越大，也越容易收敛。但是越接近输入层的网络梯度越小，收敛也就越慢。实际上，低层网络往往更加重要，因为底层网络可以细致的学习各种特征，而高层网络可以看做将这些低层网络学习到的特征进行组合。因此，当底层网络变化时，高层网络也需要重新训练。归根到底，是由于层与层之间的数据分布不同。那么，我们有没有一种方法，使得层与层之间的数据分布都比较稳定，从而快速收敛呢？

在上面的批量归一化公式中， 与 都是可以学习的参数。而对于全连接层和卷积层，归一化的过程略有不同。

对于全连接层，归一化是作用在特征维上的，也就是每一列单独计算。而对于卷积层，则是作用在通道维上的。也就是横向来看，每个像素对应的位置可能对应着多个通道，把这些通道看做小批量，然后进行归一化。

总体上看，批量归一化可以加速收敛速度，但是一般不改变模型精度。

5.11 残差网络ResNet

残差网络可以看做卷积网络中最重要的一种网络，其设计思想能够实现真正意义上的深层神经网络。下面我们首先来理解提出 ResNet 的直觉。

|575

如上图，左侧为我们传统的训练模型。每一个函数可以看做是网络的一层。随着层数的加深，在前期我们确实逐步逼近了最终的真实值。但是随着层数的增加，我们可以看到，网络似乎"学歪了"，反而离真实值越来越远。右侧是我们的残差网络，可以看到，随着层数的加深，似乎有一种定力一直让我们的网络"保持初心"。下面，我们介绍这种"定力"究竟是什么。

如上图，残差网络的设计思想就是，在输入到一块训练网络时，将自己复制一份，直接和最终的输出相加。如果输入与输出的通道数不同，就需要我们的 1*1 卷积层进行通道融合。但是输入与输出的高宽必须保持相同。

为什么这种设计能帮助我们实现更深的网络？

假设我们需要拟合 ，而输入为 ，则在这一个残差块中，我们要负责的，只是将 拟合为 0，其余的我们均不用管。因此，每个残差块都努力将当前的预测值和最终的真实值的差距缩小为 0，即使把其中一个残差块去掉，也没有影响。这就致使每个残差块有了自己专门负责的"一小部分任务"。因此，残差块往往能达到很好的效果，帮助我们构建真正意义上的深度神经网络。

|251

上图为 ResNet-18 的架构图 (卷积层和全连接层一共 18 个)

六、数据降维

5.1 PCA

https://www.bilibili.com/video/BV1Fe41157Tw?t=42.7

https://www.bilibili.com/video/BV1FT4y1E74V?t=209.4&p=88

二分分类：

设代表输入的矩阵，为第n个样本的特征矩阵

https://www.bilibili.com/video/BV1FT4y1E74V?t=6.5&p=170

https://www.bilibili.com/video/BV1Y5411c7aY?t=357.2&p=2

https://www.bilibili.com/video/BV1Yr4y1k72C?t=119.7

七、NLP

7.1 读取长序列数据

在一本书中，有成千上万个无规则的单词，前面我们利用自定义类 Vocab 将每个 Token 转化为对应的数值，那么我们如何得到每个 batch 的训练数据呢。

例如，从一本书中提取的 Token 如下：

[1, 19, 50, 40, 2183, 2184, 400, 2, 1, 19, 71, 16, 37, 11, 115, 42, 680, 6, 586, 4, 108, 7, 1420, 5, 2185, 587, 6, 126, 25, 330, 127, 439, 3, 2186, 3, 25, 1044, 362, 113, 7, 1421, 3, 1045, 1, 148, 588, 825, 3, 1, 244, 2187, 4, 1, 2188, 2189, 8, 1, 2190, 4, 589, 363, 1, 2191, 9, 826, 3, 288, 8, 75, 2192, 75, 1422, 274, 25, 2193, 2194, 3, 1423, 126, 230, 131, 2195, 6, 42, 186, 35, 3, 26, 7, 9, 2196, 116, 289, 1424, 78, 76, 2197, 2198, 827, 4, 1, 2199, 4, 2200, 3, 27, 132, 11, 6, 126, 8, 21, 114, 1425, 1, 1046, 17, 5, 1426, 1427, 14, 55, 186, 3, 2201, 2202, 25, 2203, 79, 21, 153, 681, 14, 55, 76, 11, 3, 25, 2204, 22, 85, 440, 13, 590, 2, 502, 28, 6, 2205, 31, 53, 154, 1047, 9, 91, 180, 2206, 682, 1, 828, 16, 3]

为了简化起见，我们假设序列经过精简后如下：

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]

我们面临的第一个问题是，从哪里开始划分。如果每次从固定的位置划分，如：

[0, 1, 2, 3, 4]
[5, 6, 7, 8, 9]
[10, 11, 12, 13, 14]
[15, 16, 17, 18, 19]
[20, 21, 22, 23, 24]
[25, 26, 27, 28, 29]
[30, 31, 32, 33, 34]

则有些序列永远不会被训练，如

[2, 3, 4, 5, 6]

因此，我们可以每次随机截取开头：

corpus = corpus[random.randint(0, num_steps - 1):]

现在我们成功划分得到了各种不同的句子，那么如何将其组成一个的 Batch 呢？有两种方法，分别是随机采样和顺序分区。

7.1.1 随机采样

Batch 1	Batch 2	...
Seq 4	Seq 33	...
Seq 17	Seq 49	...

可以看到，在两个 Batch 之间，句子是没有关系的。这也就是随机采样。

7.1.2 顺序分区

Batch 1	Batch 2	...
Seq 4	Seq 5	...
Seq 17	Seq 18	...

与随机采样不同，顺序分区在相邻的 Batch 之间的相同位置上语句是连贯的。

7.1 循环神经网络 RNN

要理解 RNN，关键是懂得模型的输入与输出。

例如，下面的代码是一个 RNN 的模型定义：

def rnn(inputs, state, params):  
    # inputs的形状：(时间步数量，批量大小，词表大小)  
    W_hx, W_hh, b_h, W_qh, b_q = params  
    H, = state  
    outputs = []  
    # X的形状：(批量大小，词表大小)  
    for X in inputs:  
        # 每一次循环都是一个时间步长  
        H = torch.tanh(torch.mm(X, W_hx) + torch.mm(H, W_hh) + b_h)  
        Y = torch.mm(H, W_qh) + b_q  
        outputs.append(Y)  
    out = torch.cat(outputs, dim=0)  
    return out, (H,)

假设输入的 inputs 如下 (不考虑 one-hot 编码)：

[[10, 11, 12, 13, 14]
[15, 16, 17, 18, 19]]

那么一个 batch 就含有 2 条语句，每个语句的时间步长是 5。

函数的 state 是外部输入的，有可能是全为 0 的张量 (例如随机采样)，也有可能是不为 0，比如顺序分区得到的数据，每一个 batch 与之前的 batch 是存在联系的。

在 rnn 函数里，我们可以当做数据是按列进行扫描的。每一列的时间步长的状态相同，没走过一列，就得到一列的输出。即最后的 out 为：

[
	[时间步长1的输出],
	[时间步长2的输出],
	[时间步长3的输出],
	...
]

模型的预测：

def predict_ch8(prefix, num_pred, _net, _vocab, device):  
    """在prefix后面生成新字符"""  
    state = _net.begin_state(_batch_size=1, device=device)  
    outputs = [_vocab[prefix[0]]]  
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))  
    for y in prefix[1:]:  # 预热期  
        _, state = _net(get_input(), state)  
        outputs.append(_vocab[y])  
    for _ in range(num_pred):  # 预测num_pred步  
        y, state = _net(get_input(), state)  
        outputs.append(int(y.argmax(dim=1).reshape(1)))  
    return ''.join([_vocab.idx_to_token[i] for i in outputs])

如图为预测阶段的代码。总体上看可以分成两部分。第一部分是预热，也就是初始化 state 变量。在预热期我们不用关注预测结果，因为我们的目的只是初始化 state。get_input() 函数用于选取 outputs 中的最后一个结果。

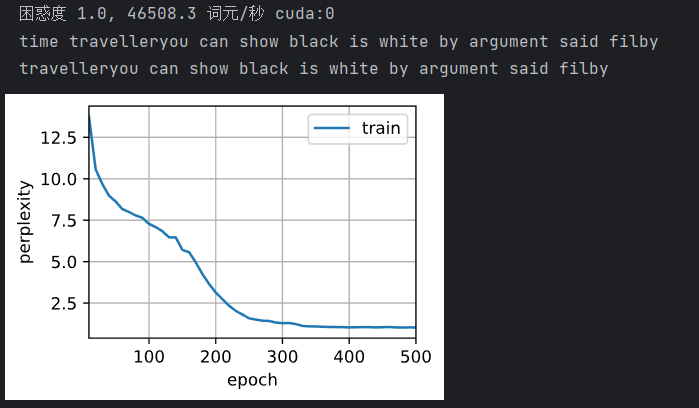
可以看到，虽然困惑度较低，但是实际的效果并不好。

7.2 门控循环单元GRU

为什么RNN在长序列上效果较差：随着序列的加长，在隐层状态中累计了太多的信息。

值得注意的是，在一个序列中，并不是每个观察值都同等重要。而GRU能够帮助隐层状态有选择的记忆(与后文的注意力机制相近)。

GRU中有两种门：

• 更新门：在计算隐层状态时，t-1时刻的隐层信息要用到多少
• 重置门：在更新候选隐层状态时要用到多少过去的信息

激活函数一般是sigmoid，因此取值在0与1之间

image-20240213231741911

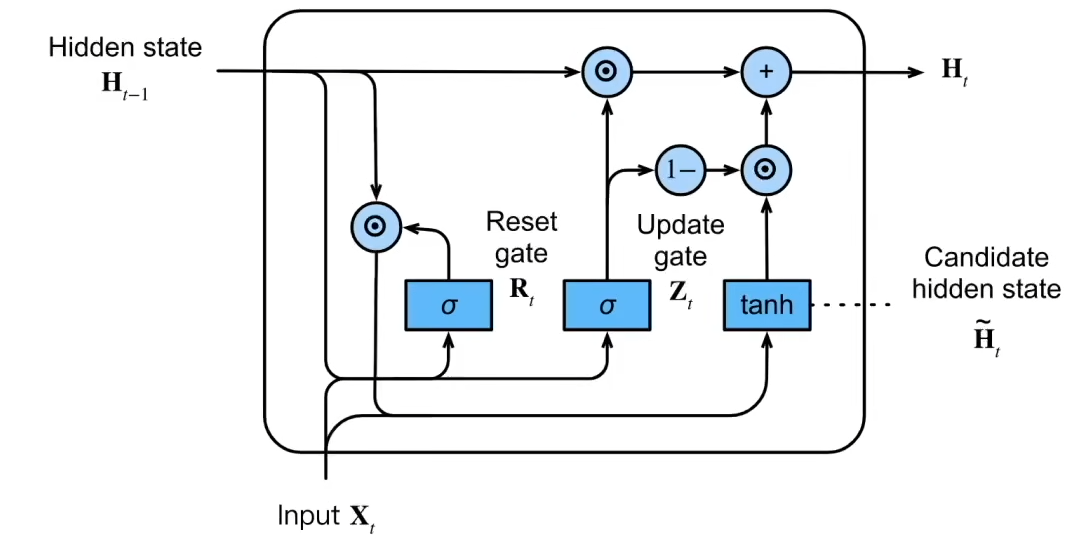
### 7.3 长短期记忆网络LSTM

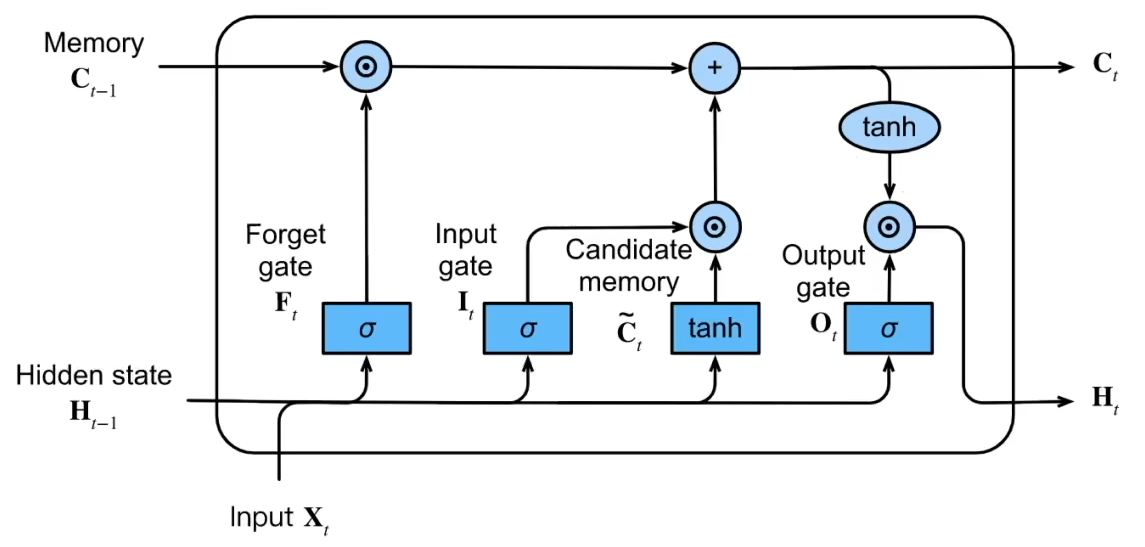
LSTM有3种网络：

• 忘记门：选择遗忘掉多少信息
• 输入门：选择吸纳多少新信息
• 输出门：选择当前时间步中的重要信息

候选记忆单元：，可以看作是长期记忆

image-20240214000030304

参考：

https://www.bilibili.com/video/BV1yb4y1T7LR?t=613.6&p=3

7.4 深层循环神经网络

7.5 双向循环神经网络

处于未来的信息也有可能很重要，比如

I am ___ hungry, I could eat half a pig.

在划线处只能填写very而不是not

image-20240214002245387

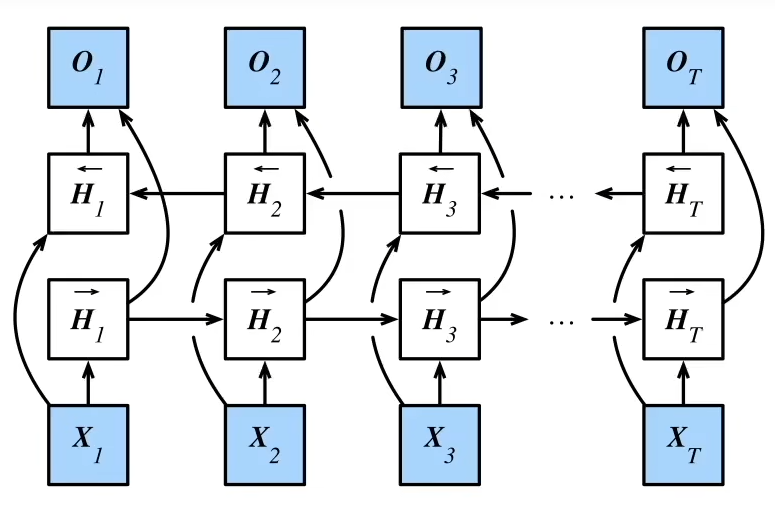
双向循环神经网络有一个特点：几乎无法推理。因为推理既需要过去的信息，又需要未来的信息。因此双向循环神经网络的主要应用是对句子进行特征提取。

7.6 机器翻译数据集

在学习机器翻译之前，我们首先需要对数据集进行处理 (注意需要考虑哪些因素)。可以分成下面几个步骤：

Step 1：对数据集进行简单的整理，如将全半角空格进行统一，将大写字母统一替换为小写字母，在标点前加上空格 (这样的话标点可以成为一个 token)。

def preprocess_nmt(txt):  
    """预处理“英语－法语”数据集"""  
  
    def no_space(char, prev_char):  
        return char in set(',.!?') and prev_char != ' '  
  
    # 使用空格替换不间断空格,使用小写字母替换大写字母  
    txt = txt.replace('\u202f', ' ').replace('\xa0', ' ').lower()  
    # 在单词和标点符号之间插入空格  
    out = [' ' + char if i > 0 and no_space(char, txt[i - 1]) else char 
           for i, char in enumerate(txt)]  
    return ''.join(out)

Step 2：将数据集进行词元化，即生成如下的格式：

[['go', '.'],
  ['hi', '.'],
  ['run', '!'],
  ['run', '!'],
  ['who', '?'],
  ['wow', '!']]

具体代码如下：

def tokenize_nmt(txt, num_examples=None):  
    """词元化“英语－法语”数据数据集"""  
    _source, _target = [], []  
    for i, line in enumerate(txt.split('\n')):  
        if num_examples and i > num_examples:  
            break  
        parts = line.split('\t')  
        if len(parts) == 2:  
            _source.append(parts[0].split(' '))  
            _target.append(parts[1].split(' '))  
    return _source, _target

Step 3：生成词汇表，即 id2word，word2id

src_vocab = d2l.Vocab(source, min_freq=2, reserved_tokens=['<pad>', '<bos>', '<eos>'])

Step 4：进行截断或填充

def truncate_pad(line, num_steps, padding_token):  
    """截断或填充文本序列"""  
    if len(line) > num_steps:  
        return line[:num_steps]  # 截断  
    return line + [padding_token] * (num_steps - len(line))  # 填充  
truncate_pad(src_vocab[source[0]], 10, src_vocab['<pad>'])
# [47, 4, 1, 1, 1, 1, 1, 1, 1, 1]

可以看到，这里用到了词汇表，Vocab 类中的 __getitem__ 方法可以很方便的将 Token 转化为索引。

Step 5：获取迭代器

def build_array_nmt(lines, vocab, num_steps):  
    """将机器翻译的文本序列转换成小批量"""  
    lines = [vocab[l] for l in lines]  
    lines = [l + [vocab['<eos>']] for l in lines]  
    array = torch.tensor([truncate_pad(l, num_steps, vocab['<pad>']) for l in lines])  
    valid_len = (array != vocab['<pad>']).type(torch.int32).sum(1)  
    return array, valid_len
src_array, src_valid_len = build_array_nmt(source, src_vocab, num_steps)  
tgt_array, tgt_valid_len = build_array_nmt(target, tgt_vocab, num_steps)  
data_arrays = (src_array, src_valid_len, tgt_array, tgt_valid_len)  
data_iter = d2l.load_array(data_arrays, batch_size)

综上，对于 NLP 相关的数据处理，大体上可以分为 5 步：数据规整 (大小写，空格)，词元化，词汇表构建，填充和截断，获取迭代器。

7.7 编码器和解码器

在机器翻译中，输入和输出都是可变长序列，但是在之前的 RNN 中，我们的句子长度都是固定的。那么有没有方法可以让我们处理可变长序列呢？这就引出了我们的编码器和解码器架构。

可以看到，输入和输出其实都可以处理变长序列，可以看做两个 RNN。

7.8 Seq2Seq

Seq2Seq 也就是语句到语句，利用了前文的编码器和解码器架构。编码器这一侧，主要使用了嵌入层和 RNN 层。不需要全连接层，只需要把隐藏层的状态进行输出即可。

class Seq2SeqEncoder():
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0,):
        # 嵌入层
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size, num_hiddens, num_layers,
                          dropout=dropout)

    def forward(self, X, *args):
        # 输出'X'的形状：(batch_size,num_steps,embed_size)
        X = self.embedding(X)
        # 在循环神经网络模型中，第一个轴对应于时间步
        X = X.permute(1, 0, 2)
        # 如果未提及状态，则默认为0
        output, state = self.rnn(X)
        # output的形状:(num_steps,batch_size,num_hiddens)
        # state的形状:(num_layers,batch_size,num_hiddens)
        return output, state

在解码器这一侧，需要将编码器的最后时刻的隐状态 (batch_size * num_hiddens) 复制时间步长份，然后将输入与隐状态进行拼接，再放入到 RNN 中。

class Seq2SeqDecoder():
    """用于序列到序列学习的循环神经网络解码器"""
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0,):
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, *args):
        return enc_outputs[1]

    def forward(self, X, state):
        # 输出'X'的形状：(batch_size,num_steps,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        # 广播context，使其具有与X相同的num_steps
        context = state[-1].repeat(X.shape[0], 1, 1)
        X_and_context = torch.cat((X, context), 2)
        output, state = self.rnn(X_and_context, state)
        output = self.dense(output).permute(1, 0, 2)
        # output的形状:(batch_size,num_steps,vocab_size)
        # state的形状:(num_layers,batch_size,num_hiddens)
        return output, state

预测序列评估指标：Blue

从公式中可以看到，Blue 综合了长短序列。若输出较短，则左侧部分会很小。若输出序列较长，虽然概率会比较小，但是其指数也比较小，因此右侧部分会比较大。Blue 指标越大越好。

7.9 束搜索

前面我们预测某一个时间步的输出时，往往需要选择概率最大的单词。但是，局部最优不一定全局最优。0.5 * 0.4 = 0.2 但是 0.4 * 0.9 = 0.36。即若我们选择概率比较小的 0.4，下一刻可能会遇到概率比较大的 0.9。因此，为了全局最优，我们引出了束搜索。

值得一提的是，束搜索虽然不能实现全局最优，但是能够在局部最优和全局最优之间做一个平衡。

综上，有超参数 k，在第一步选取最优的 k 个单词，往后在这 k 个序列中，此后都是正常的贪心算法，不再递归执行束搜索。

那么，最终得到的 k 个序列，如何评估哪个序列最好呢？

一般来说，参数 。对概率取对数后变成了负数。对于更长的序列， 越大，因此 越小，因此最终会更接近 0，得分越高。

7.10 注意力机制

7.10.1 注意力机制的概念

当我们随意漫游在一间屋子中，往往会被屋子中最突出的物品吸引，这就是不随意线索 (不随意识的线索)。然而，如果我们此刻想在屋子中寻找一本书，那么自然而然的我们会更加关注书本，这就是随意线索 (有主观意识的搜索)。那么，我们如何将这种思想引入到深度学习领域呢？

假设我们现在有很多 key-value 对，有一个新的键 query，现在需要根据 query 计算对应的值。自然的，如果 key-value 对中有与 query 相同的键，我们就可以直接输出对应的值。但是如果没有呢？我们需要对各个 value 取平均吗？这不是一个好的想法，因为不同的 key-value 值得我们注意的重要性并不同。

符合直接的做法是，如果一个 key 与我们的 query 相似，也就是注意力分数高，我们就对其对应的 value 赋予更高的注意力。我们对每一个 key 都计算一个注意力分数，然后经过 softmax 归一化，最后对 value 加权求和，不就得到我们想要的值了吗？

观察上面的数学表达，其中 是一个核。整体上也就是一个赋权求和。关键是 是什么。

若 是一个高斯核：

则经过化简后可以类似 Softmax，只不过对输入进行了变换。

计算结果：

显然，这种方法不需要经过训练，没有学习的参数。最终的结果并不太好。

通过注意力的热力图我们可以看到，这种方法的注意力过于分散。

接下来，我们引出可以经过学习的参数，即：

经过训练后，得到了如下的拟合效果：

可以看到，拟合效果明显更好。

而从注意力的热力图可以看到，注意力更加集中，也就是每一个输入的数据，更加关注周围的数据。

而这种思想其实可以很好的用在 Seq2Seq 模型中。因为在使用注意力机制以前，解码器使用的是编码器的最后一层的最后一个时间步长的隐层状态。但是当句子很长的时候，这个隐状态不一定能保存句子的所有信息。

7.10.2 注意力分数

前面我们使用了高斯核来进行建模。试试上其指数部分可以看做注意力评分函数。也就是我们的 query 和 key 的相似程度。接下来我们介绍两种注意力平分函数。

首先是加性注意力。

当 key，value，query 各自的维度不同，例如：

设参数：

其中参数 和 分别可以将 query 和 key 映射到空间

然后是缩放点积注意力。

如果能够直接点积的话效率自然会提高不少，但是这种方法要求 query 和 key 的维度相同 (例如都为 d)。

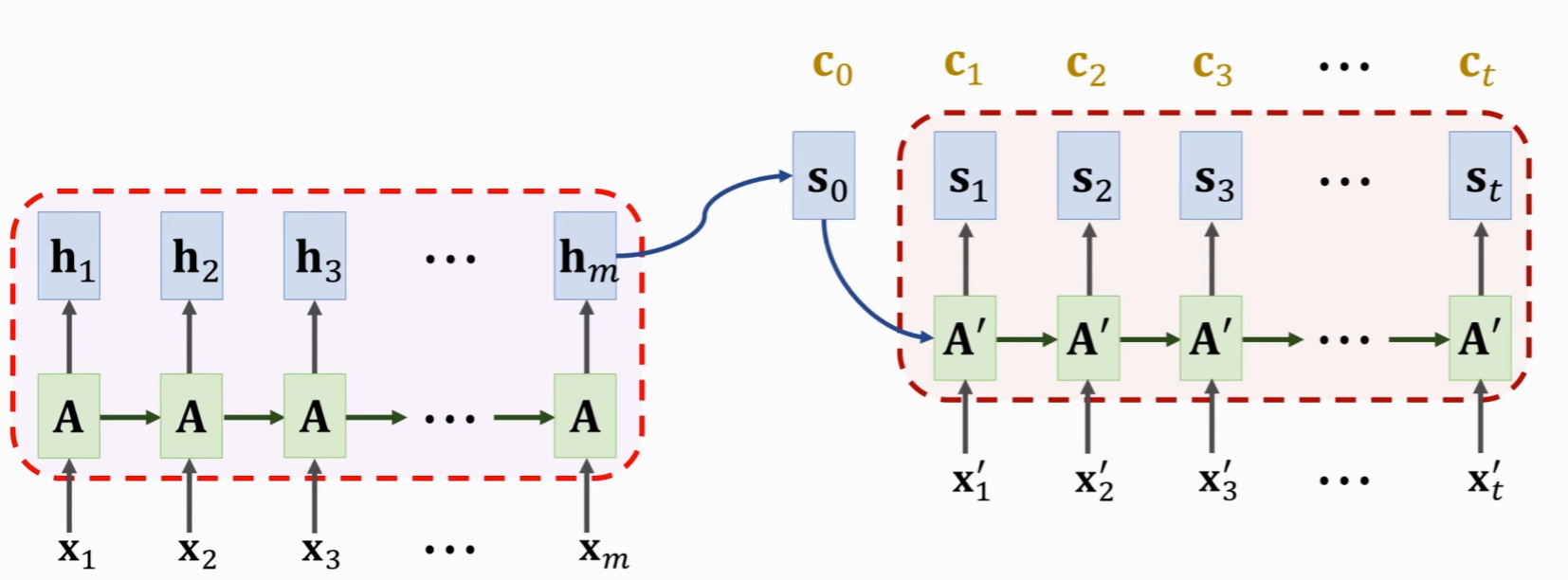
7.10.3 注意力机制与 Seq2Seq

前文的 Seq2Seq 模型中，我们对于解码器的输入，应用的是输入 x 与编码器的隐状态的拼接。然而，引入了注意力机制后，与 x 拼接的变成了上下文状态 ：

而关于权重的计算有很多方法，可以自行选择。

注意，对于状态 s，可以去除，只让输入 x 与上下文变量 c 进行 concat。

7.11 自注意力机制

7.11.1 原理

前面的注意力机制应用在两个 RNN 上面，其中的 key、query、value 各不相同。然而，在自注意力机制中，key 、query 和 value 都是相同的。即：

因此，自注意力机制可以实现并行计算。

但是，虽然可以并行计算，却没有位置信息，也就是对于自注意力层来说，每个位置都没有区别。下面，我们讲解如何加入位置信息。

对于第 i 个时间步的单词对应的词向量，第 j 列对应的偏移：

假设 i 不变，则对于词向量的奇数列和偶数列，偏移分别使用 sin 和 cos。

7.11.2 自注意力机制与 Seq2Seq

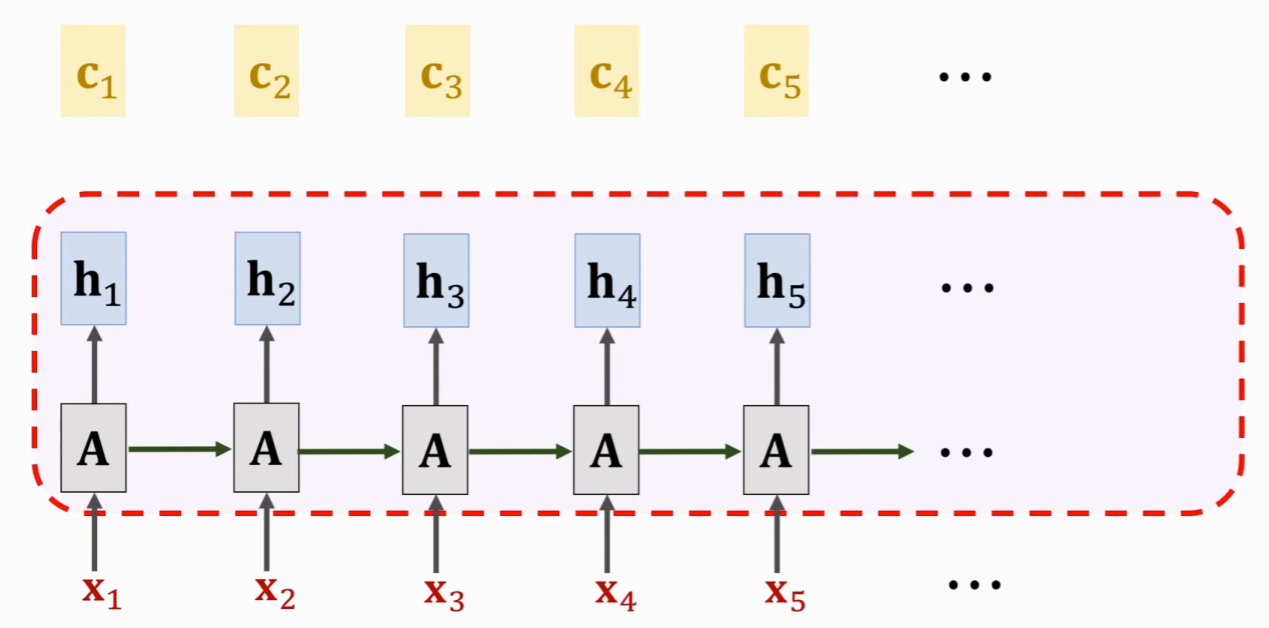
Self-Attention 是应用在单 RNN 上面的，而 Attention 应用在两个 RNN 上面。

对于传统的 RNN，隐层状态更新如下：

而对于使用自注意力机制的 RNN，则隐层状态更新如下：

其中 是对以往的隐藏状态的加权平均。

7.11.3 发展历史

注意力机制：2015，Neural machine translation by jointly learning to align and translate

自注意力机制：2016，Long short-term memory-networks for machine reading

7.12 Transformer 模型

Transforer 只有全连接层和注意力层，并没有 RNN。目前主流的机器翻译往往使用 Transformer 模型+BERT。

Transformer 使用了编码器和解码器的架构。

7.11.1 Attention

7.11.2 Self-Attention

7.12 Bert

7.13 ViT