现代密码学

现代密码学

慕课：https://www.icourse163.org/spoc/course/UESTC-1450239182

慕课答案：https://vip.studypro.club/2021/2021%e7%9f%a5%e5%88%b0%e7%ad%94%e6%a1%88-%e7%8e%b0%e4%bb%a3%e5%af%86%e7%a0%81%e5%ad%a6-%e6%9c%80%e6%96%b0%e4%b8%ad%e5%9b%bd%e5%a4%a7%e5%ad%a6mooc%e6%bb%a1%e5%88%86%e7%ab%a0%e8%8a%82%e6%b5%8b%e8%af%95/

密码：15891515632

期末

判断题，4题，共20分 简答题，4题，共20分 计算题，3题，共30分 综合题，2题，共30分

一、概述

1.1 密码学的基本概念

  • 信息安全的基本属性/密码学可解决的信息安全问题：
  • 机密性：也就是别人看不到或者看不懂，保证信息为授权者使用而不泄露给未经授权者
  • 完整性：就是数据完整性和系统完整性
  • 不可否认性：发送方和接收方都不能抵赖进行的传输
  • 认证：就是消息来源和通信实体的真实性
  • 可用性：保证系统随时为授权者服务，不会出现非授权者滥用却对授权者拒绝服务的情况
  • 其它：可靠性，可控性，审计
  • 攻击手段的分类：
    • 被动攻击
      • 定义：试图了解或利用系统的信息但是不影响系统资源
      • 消息泄露
      • 流量分析
    • 主动攻击
      • 定义：试图改变系统资源或影响系统运作
      • 假冒
      • 重放
      • 消息篡改
      • 拒绝服务
  • 密码算法的组成：
    • 明文M
    • 密文C
    • 密钥k
    • 加密函数E
    • 解密函数D
  • 密码算法的需求：
    • 可逆：算法使用者可以将密文恢复成明文
    • 不可逆：攻击者无法将密文恢复成明文
  • 一个好的密码体制至少应满足的两个条件：
    • 已知明文m和加密密钥时，进行加密很容易；已知密文c和解密密钥时，进行解密很容易；
    • 在不知道解密密钥时，不可能由密文c恢复出明文m
  • 密码算法的分类(按功能)：
    • 加密算法
    • 杂凑函数
    • 数字签名
  • 密码算法的分类(按使用方式)：
    • 对称密钥密码
    • 无密钥密码
    • 非对称密钥密码

1.2 中国古代密码艺术

  • 中国民间艺术：
    • 图画传情
    • 会意诗
    • 藏头诗
    • 叠痕法
    • 漏格板加密法
  • 中国古代军事密码：
    • 阴符
    • 阴书
    • 反切法
  • 中国近代密码：
    • 密本型
    • 加乱型

1.3 外国古代密码艺术

  • 代替密码
    • 凯撒密码：用明文的后面第三个字母替代
  • 换位密码
  • 密码机

1.4 密码学发展简史

密码学发展的3个阶段：

  • 古代密码1800以前

    密码学家常常是凭直觉和信念来进行密码设计和分析，而不是靠推理证明，数据的保密更多的是基于加密算法的保密，而密码工作者多为语言学家和猜谜高手。常见的有凯撒密码，维吉尼亚密码，天书密码

  • 近代密码1800-1949

    密码机迅速发展，越来越多的数学工作者加入了密码学的队伍，常见的有密码机

  • 现代密码

古典密码的特点：

  • 密码学还不是科学，更多的是艺术
  • 出现了一些密码算法和加密设备
  • 出现密码算法的基本手段：代替和置换
  • 数据的保密更多的是对加密算法的保密

密码学的两个分支：

  • 密码编码学

  • 密码分析学

    目标：

    • 恢复密钥
    • 恢复合法密文对应明文

1.5 密码分析学

常见攻击方法：

  • 穷举攻击：试遍所有的密钥
  • 统计分析攻击：通过分析密文和明文的规律来破译
  • 解密变换攻击：通过数学求解找到解密变换

常见攻击分类：

  • 唯密文攻击：攻击者只有一些密文
  • 已知明文攻击：攻击者知道一些明文和对应的密文
  • 选择明文攻击：攻击者有加密机的权限，能够设计一些明文获取密文
  • 选择密文攻击：攻击者有解密机权限，可以选择一些密文获取明文

无条件安全：

  • 无论截获多少密文，都没办法确定明文

计算上安全：

  • 使用有效资源对密码系统进行分析而未能破译

密码算法要满足的准则：

  • 破译密文的代价远超被加密信息的价值
  • 破译密文的时间超过信息的有效期

1.6 古典密码算法

置换密码：

  • 把字母的顺序进行变换

单表代替密码：

  • 加法密码

    例：凯撒密码(k=3)

  • 乘法密码

  • 仿射密码

多表代替密码：

  • 必要性：由于单表代替密码只要明文一样，密文就一样，因此避免不了统计分析，故引入多表代替密码

  • 维吉尼亚密码：

  • 更常用的形式：

    为明文分组，(A,B)为密钥，且

    解密：

    如何求逆矩阵？伴随矩阵法

二、流密码

注意点：

  • 流密码里面的是GF(2)上的加法！不是异或！

本章节大致可分为五个部分：

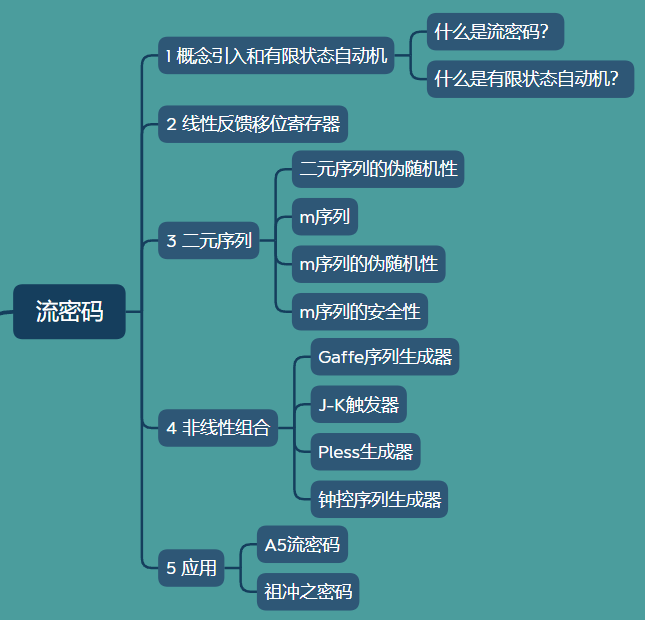
image-20230519163448816

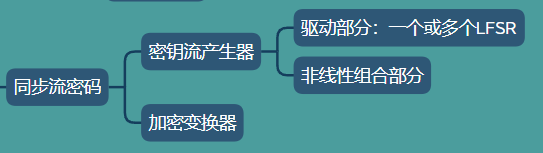
主要讲的是同步流密码，同步流密码的组成如下：

image-20230519165320086

2.1 概念引入和有限状态自动机

2.1.1 流密码

一次一密：

  • 密钥是随机生成的，并且只用一次
  • 优点：
    • 密钥随机生成，并且只用一次
    • 无条件安全
    • 加密和解密为加法运算，效率高
  • 缺点：
    • 密钥长度要和明文一样长，密钥共享困难，不实用

流密码：

  • 又称序列密码，可以用移位寄存器电路实现，主要基于硬件实现
  • 基本思想：利用密钥k产生一个密钥流，然后加密；密钥流由密钥流发生器产生，，为加密器中的记忆元件在时刻i的状态

同步流密码：

  • 内部记忆原件的状态独立于明文字符，因此可将同步流密码的加密器分为密钥流产生器和加密变换器两部分
  • 二元加法流密码是目前最常用的流密码体制，加密变换可表示为
  • 若密钥用作滚动密钥流，则加法流密码就退化成一次一密
  • 良好的滚动密钥生成器应包含以下性质：
    • 极大的周期
    • 良好的统计特性
    • 抗线性分析，具有高线性复杂度
    • 足够混淆
    • 足够扩散
    • 抵抗不同形式的攻击

2.1.2 有限状态自动机

有限状态自动机：

  • 是具有离散输入输出的一种数学模型

  • 组成：

    • 有限状态集S
    • 有限输入字符集和有限输出字符集
    • 转移函数，

  • 表示：转移图

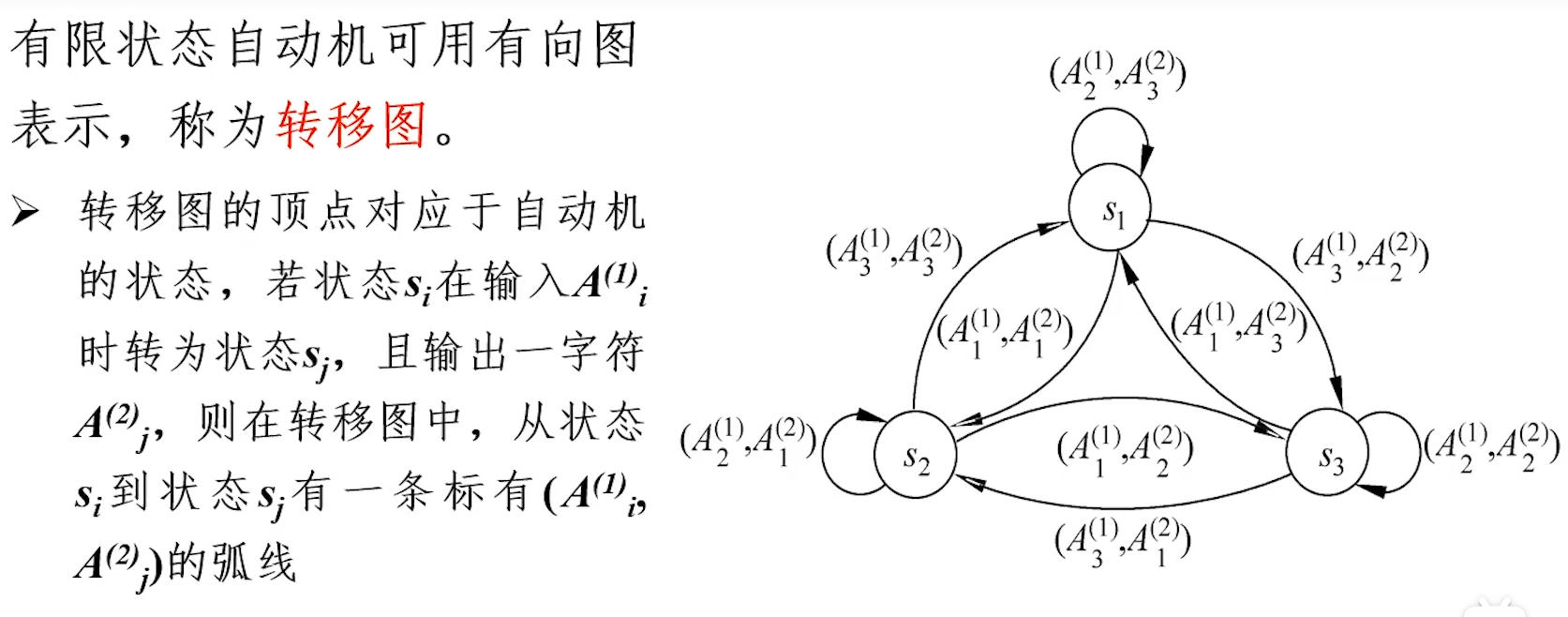
    image-20230513200357184

密钥流产生器：

  • 参数为k的有限状态自动机
  • 关键在于：找到适当的状态转移函数和输出函数，使得输出序列z满足随机性条件，并且容易实现；一般采用线性的和非线性的
  • 组成：
    • 驱动部分：控制状态转移，并向非线性组合部分提供序列
    • 非线性组合部分：利用序列组合出满足要求的密钥流序列
  • 目前最流行和使用的密钥流产生器，驱动部分是一个或多个线性反馈移位寄存器

2.2 线性反馈移位寄存器

反馈移位寄存器：

  • GF(2)上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数组成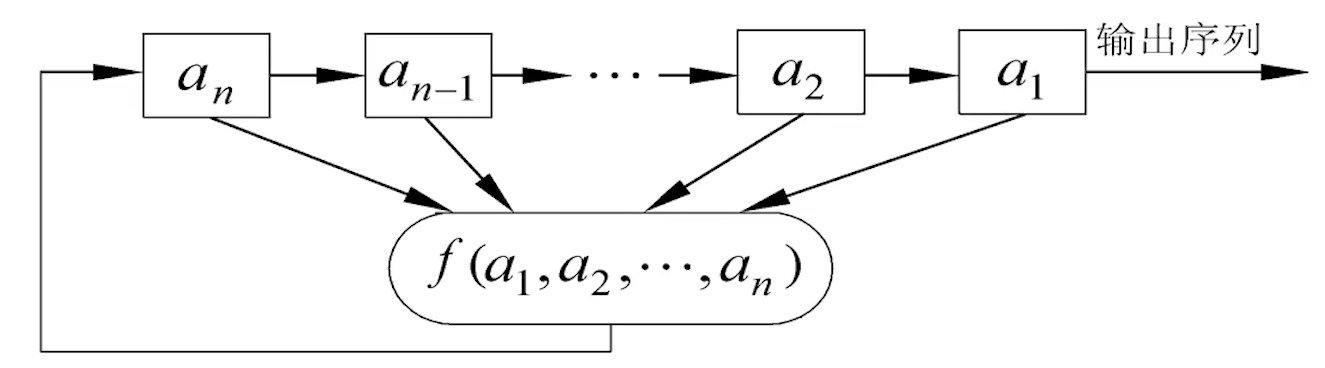

  • image-20230513211049249

  • 反馈函数：n元布尔函数，也就是自变量和因变量只取0和1

线性反馈移位寄存器LSFR：

  • 总是假定中至少有一个不为0，总是假定

  • n级LFSR的状态周期：

  • 输出周期＝状态周期

  • 周期达到最大值的序列为m序列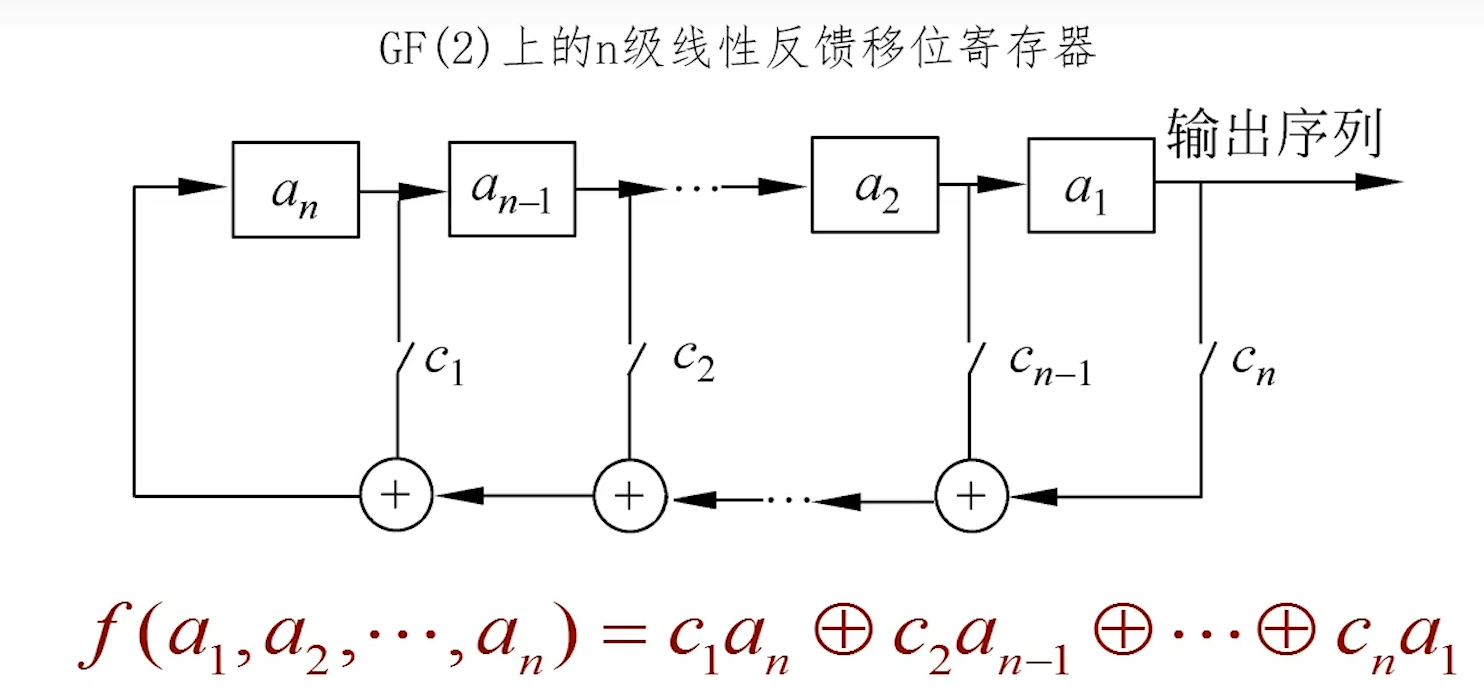

  • image-20230513222309903

参考资料：https://zhuanlan.zhihu.com/p/366067972

2.3 二元序列

2.3.1 二元序列的伪随机性

主要内容：

  • 密钥流产生器产生什么样的序列才能满足要求？

二元序列：

  • GF(2)上的一个无限序列

  • 周期：最小正周期记为

  • 游程：100001：0的4游程，01110，1的3游程

  • 自相关函数：

    当t=0时，R(t)=T；当t≠0时，称R(t)为异相自相关函数

  • 3个随机性公设：

    • 在序列的一个周期内，0与1的个数相差至多1(也就是序列中0和1出现的概率基本上相同)
    • 在序列的一个周期内，长为i的游程占游程总数的，且在等长的游程中0和1的个数相同(也就是每个位置上0和1出现的概率相同；注意，长度为i的游程在伪随机序列中符合指数分布)
    • 异相自相关函数是一个常数(描述序列与其平移后的序列的相似程度)

伪随机序列的定义：

  • 若对于一切，有，则称序列a为伪随机序列
  • 还应满足的条件：
    • 周期足够大
    • 序列易高速生成
    • 具有不可预测性，也就是知道一部分无法分析整个序列

2.3.2 m-序列

主要讲了m序列的判定条件

LFSR的一元多项式表示：

  • 定义：n级线性移位寄存器的输出序列满足递推关系

  • LFSR的特征多项式：

  • 什么是特征多项式：就是LFSR的反馈多项式中的系数组合成的多项式

  • G(p(x))：由递推关系产生的非0序列有个，称其全体为G(p(x))

  • 给定序列，称之为序列的生成函数

  • 定理：

    是上的多项式，中任一序列的生成函数满足其中

  • 定理：

    说明n级LFSR产生的序列可以用级数更多的LFSR产生

  • 定义：设p(x)为GF(2)上的多项式，使成立的最小正整数p称为p(x)的周期或阶

  • 定理：若序列的特征多项式p(x)定义在GF(2)上，p为p(x)的周期，则的周期r|p

    说明n级LFSR输出序列r不依赖于初始条件，而依赖于特征多项式p(x)

  • 定理2.4 设p(x)为n次不可约多项式，周期为m，序列，则的周期为m

  • 定理2.5 n级LFSR产生的序列有最大周期的必要条件是其特征多项式是不可约的

  • 定义2.4 若n次不可约多项式p(x)的阶为，则称p(x)为n次本原多项式

  • 定理2.6 设，为m序列的充要条件是p(x)为本原多项式

2.3.3 m-序列的伪随机性

定理：

https://www.bilibili.com/video/BV1Gx411f7Yo?t=234.1&p=13

  • GF(2)上的n长m序列满足如下性质：

    • 一个周期内，有0,1出现的次数分别为和

    • 一个周期内，总游程数为，对于，长为i的游程有个，且0,1游程各半；长为n-1的0游程一个，长为n的1游程1个

    • 的自相关函数为

2.3.4 m-序列的安全性

已知一段序列能否求出相对应的反馈多项式呢？

  • 解方程

    要求已知是n位线性移位寄存器，并且知道连续2n位

    • 普通算式
    • 列矩阵

  • 线性反馈移位寄存器综合解：BM算法

    • BM算法可以类比归纳法，是逐级递推得到的

    • 流程：

      对于n从0到N-1：

      • 首先计算，？

        • 若：

        • 若：

          • 若：

          • 若：

参考资料：https://blog.csdn.net/qq_47912072/article/details/112688483

2.4 非线性组合

  • Gaffe序列生成器：

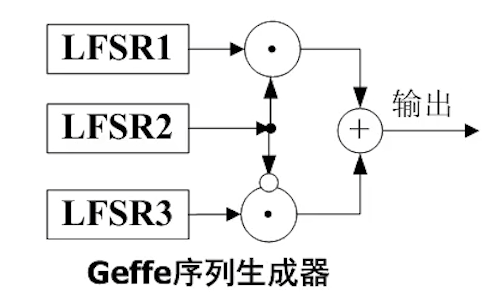
    • image-20230514095627298

    • 当LFSR2输出为1，输出LFSR0，否则输出LFSR3

    • 若LFSRi的输出序列为，则输出序列可表示为：

    • 设LFSRi的特征多项式分别为次本原多项式，且两两互素，则Gaffe的周期：

      线性复杂度：

  • J-K触发器：

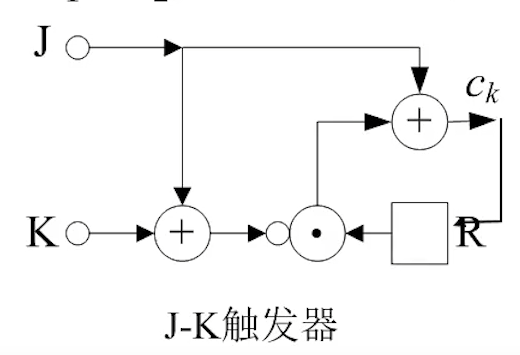
    • image-20230514100456690

    • 真值表：

      J K
      0 0
      0 1 0
      1 0 1
      1 1

    • 输出表达式：

      其中分别是J和K端的输入

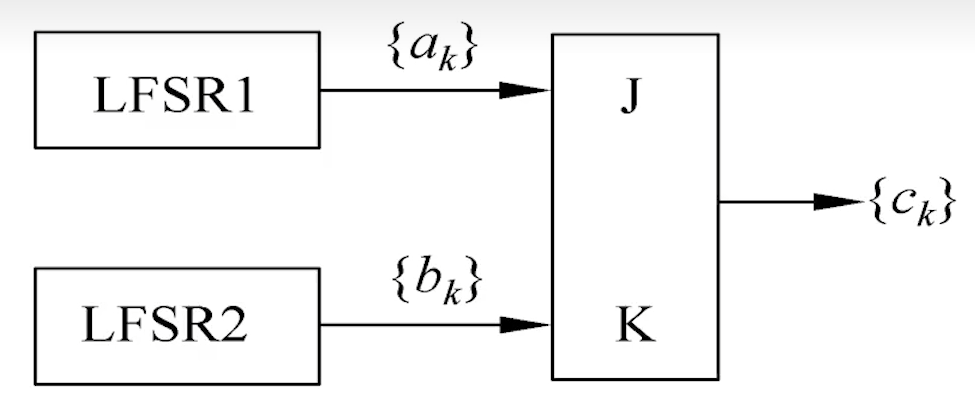
    • image-20230514101015419

      当为m级m序列，为n级m序列，且m与n互素，时，的周期为

    • 弱点：

      所以一旦知道两个相邻位，就可以推断出来和中的一个，一旦知道足够多的此类信息，就可通过密码分析的方法得到和两个序列

      为了克服上述缺点，Pless提出了由多个J-K触发器序列驱动的多路复合方案，也就是Pless生成器

  • Pless生成器：

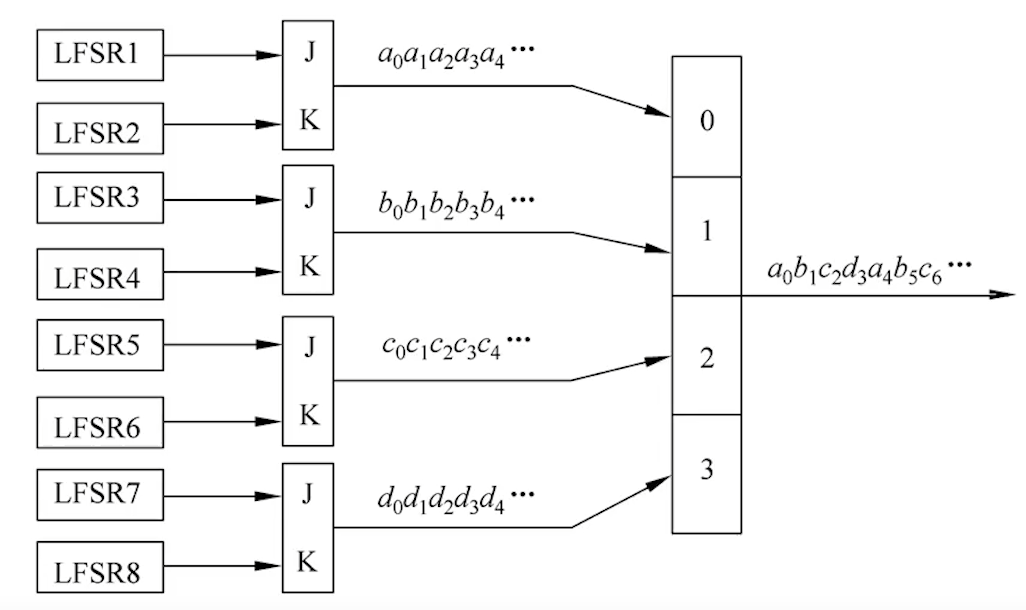
    • image-20230514101821789

    • 由8个LFSR，4个J-K触发器和一个循环计数器构成

  • 钟控序列生成器：

    • image-20230514102104634

    • 主要是由一个LFSR控制另一个LFSR；当LFSR1输出1，LFSR2通过移位产生下一位；当LFSR输出0，LFSR2重复输出当前位

    • 设LFSR1和LFSR2的序列分别为和，周期分别为和，假设钟控序列的周期为，可得如下关系：

      其中

    • 的一个周期至少是LFSR1和LFSR2同时回到初始状态的时刻，也就是周期至多是

    • LFSR1运行一个周期，LFSR2运行拍，，则LFSR1运行个周期后，LFSR刚好运行拍，也就是个周期，这时候两个LFSR都回到初始态，运行了个节拍

    • 若和的极小特征多项式分别为GF(2)上的m和n次本原多项式和，且，则，而为一个周期内1的个数，因此，故，所以

    • 可推导出的线性复杂度为，极小特征多项式为

2.5 应用

2.5.1 A5流密码算法

  • 基本用法
    • 一般用于蜂窝式移动电话系统语音和数字加密
    • 基本密钥：预置在SIM卡中，与基站1共享，一旦植入SIM卡便无法改变
  • 基本原理
    • 每次会话时基站会产生一个64bit的随机数k，使用其它密码算法将k加密传给用户手机，k仅用于一次通话时间
    • 明文处理：按照每帧228bit加密
    • 加密方式：
      • 对每帧使用不同的帧密钥
      • 帧会话密钥：帧序号，22bit

2.5.2 祖冲之密码

初始化步骤：

graph LR

A(密钥装入)-->B(R1,R2置0)
B-->C(BR)
C---->D(非线性函数F)
D---->E(LFSR初始化模式)
E-->|32轮|C

工作步骤：

graph LR
BR(BR)-->F("F(X0,X1,X2)")
F-->LFSR(LFSR工作模式)
LFSR-->BR2(BR2)
subgraph one
BR2-->|L轮|Z("Z=F(X0,X1,X2)异或X3")
Z-->LFSR2("LFSR工作模式")
LFSR2-->BR2
end one
Z-->RST("密钥字")

三、分组密码

3.1 基本概念

定义：

  • 明文序列是一个比特流，和流密码的区别就是分组密码是一组一组的加密，设分组长度为n

    密文分组长度是m，这种密码实质上是字长为n的数字序列的代换密码

    通常取n=m

    若n<m：有数据拓展的分组密码

    若n>m：有数据压缩的分组密码

安全性设计原则：

  • 混淆原则

    就是将密文明文密钥之间的统计关系和代数关系变得尽可能复杂

  • 扩散原则

    让明文中的统计规律和结构规律散射到相当长的一段统计中去

分组密码算法应满足的要求

  1. 分组长度n要足够大
  2. 密钥量足够大
  3. 由密钥确定置换的算法要足够复杂
  4. 加密和解密运算简单
  5. 数据拓展
  6. 差错传播尽可能小

分组密码的实现原则

  • 软件实现的原则：
    • 使用子块和简单的运算，避免用以软件难以实现的逐比特置换
  • 硬件实现的原则：
    • 加密解密可用同样的器件来实现

3.2 SP网络

  • 定义：

    • S指的是替代，P指的是置换，SP网络又称为代换网络

    • 若明文和密文的分组长度都是n，则不同的可逆变换的个数有个，明文的每一个分组有个取值

    • 如果分组长度足够小，系统则等价于古典的代换密码，容易通过明文的统计分析而被攻破

  • 一般的，对于n比特的代换结构，密钥的大小是比特

  • 代换网络：

    • 代换是输入集A到输出集A'上的双射变换：，k是控制输入变量，也就是密钥

    • 全代换网络：若网络可以实现所有可能的个代换，则称为全代换网络，全代换网络密钥个数必须满足

    • 代换的集合：，在实际应用中，S中元素的个数远小于

  • 代换盒(S盒)：

    • 在密码设计中，可选，将设计n个变量的代换网络化为设计个较小的子代换网络，每个子代换网络只有个输入变量，称每个子代换网络为代换盒。

3.3 Feiste密码结构

设计思想：

  • 乘积密码是指顺序地执行两个或者多个密码系统，使得最后的密码强度高于每个基本密码系统产生的结果

  • 输入是分组长为2w的明文和秘钥K，每组明文分为两部分，在进行完n轮迭代后，左右两半再合并在一起产生密文分组(记住通式)：

    是第i轮用的子密钥，由加密密钥K得到

  • Feist解密过程是和加密过程一样的，只不过采用密文作为输入，但是使用的子秘钥的次序和加密过程相反

3.4 DES算法

  • 有两种挫败统计系统的方法：

    • 扩散：在密文中隐秘明文的统计特征，比如在32位的数据中选择16位扩散成2位

    • 混淆：让密钥和密文的关系变得复杂，本质是加入非线性关系

  • DES的分组长度为64bits，密钥也是64bits，但是有8bits奇偶校验位

  • 什么是对合变换？

    • 就是F(a)=b，F(b)又能变回a

  • 算法主要步骤：

    • 初始置换：也就是分组内的字节顺序打乱

    • 16轮迭代的乘积变换

      • E盒拓展(32bit转换成48bit)
      • 和子密钥异或
      • S盒压缩(核心)(48bit转换成32bit)
      • P盒置换

      流程图：

      graph TB
subgraph 1
L0("L0(32bit)")
R0("R0(32bit)")
end
subgraph 3
L1(L1)
R1(R1)
end
R0-->L1
subgraph 2
R0-->E("E拓展(32bit-->48bit)")
E-->X("与子密钥异或(48bit-->48bit)")
X-->S("S盒(48bit-->32bit)")
S-->P("P置换(32bit-->32bit)")
P-->X2(异或)
end
L0-->X2
X2-->R1

    • 逆初始置换

  • S盒的具体解释：

    • 作用：

      对数据进行压缩

    • 例：

      原始数据为111111，头尾数据为11，转成十进制为3，即为行数；中间部分为1111，转成十进制为15，即为列数

  • 密钥如何编排：

    • 64bit->56bit：PC-1置换选择器除去奇偶校验位

    • 56bit->48bit：PC-2置换选择器

    • 思维导图：

      graph TB
B(密钥64bits) --> C(置换选择PC1除去8个校验位得到56bit)
C --> D("C<sub>i</sub>(28bit)")
C --> E("D<sub>i</sub>(28bit)")
D --> F("循环左移ibit")
E --> G("循环左移ibit")
F --> H("置换选择PC2(56bit)")
G -->H

DES参考资料：

DES加密算法｜密码学｜信息安全

密钥编排

3.5 DES的安全性

  • 常见攻击方式：

    • 唯密文攻击：只知道密文
    • 已知明文攻击：得到了一些明文和对应的密文
    • 选择明文攻击：就是可以自己构造一些明文，得到对应的密文，也就是攻击者具有加密机的权限
    • 选择密文攻击：可以自己构造一些密文，得到其明文，也就是攻击者具有解密机的权限
    • 选择文本攻击：可以制造任意的明文/密文，得到对应的密文/明文

  • DES相关(请分析DES的安全性)：

    • 互补性：

      若明文组和密钥k都逐位取补，则密文也会逐位取补；这种特性让选择明文攻击的工作量减半

    • 弱密钥和半弱密钥：

      弱密钥：，DES存在4个弱密钥，就是加密两次又变回原来的

      半弱密钥：，至少有12个半弱密钥，就是密钥等价

  • 弱密钥：

    定义：若给定初始密钥k，各轮的子密钥都相同，则称k为弱密钥；因此，有4个弱密钥：全0，全1，左0右1，左1右0

    缺点：让选择明文攻击下的工作量减半

3.6 3DES

  • 定义：

    多重DES就是使用多个密钥利用DES对明文进行多次加密，多重DES可以增加密钥量

  • 分类：

    • 双重DES
    • 三重DES

  • 双重DES：

    可将密钥长度拓展为112bit

    graph LR
M(明文)-->D1(DES1)-->D2(DES2)-->C(密文)

    但是会有中间相遇攻击：

    • ，则
    • 先从的个可能取值中对明文x加密，将密文z存储在表中；然后从的个可能取值中对密文y解密，若从表中找到相匹配的值，则可确定两个密钥

    中间相遇攻击的复杂度：

  • 三重DES：

    • 定义：

      类似双重DES，但是三个密码组件既可以是加密函数，也可以是解密函数；

      当，则称为双密钥三重DES(推荐)

    • 算法：

      常称为加密-解密-加密方案，简记为EDE方案

    • 安全性：

      破译的穷举密钥搜索量为量级

      差分分析也要超过量级

3.7 分组密码的工作模式

  • 工作模式定义：

    根据不同的数据格式和安全性要求，以一个具体的分组密码算法为基础构造一个分组密码系统

  • 五种工作模式

    • 电码本模式ECB：

      • 定义：就是各个分组是独立的，加密方式相同
      • 优点：
        • 实现简单
        • 不同分组可并行加密，用硬件实现时速度很快
      • 缺点：
        • 相同明文分组对应相同密文分组
        • 不能隐蔽明文分组的统计规律和结构规律，不能抵抗替换攻击
      • 应用(消息较短的时候)：
        • 用于随机数的加密保护
        • 用于单分组明文的加密

    • 密码分组链接模式CBC：

      • 定义：先将明文分组与上一次的密文块异或，然后加密处理。这种模式必须选择一个初始向量用于加密第一块明文；

        加密过程：

        解密过程：

        graph LR
Ci-1(c0)-->O((+))
Mi(m1)-->O
O-->DES(DES加密)
DES-->C1(c1)

      • 优点：

        • 明文块的统计特性得到了隐蔽

        • 具有有限的错误传播特性

          一个密文块的错误将导致两个密文块不能正确解密

        • 具有自同步功能

          密文出现丢块和错块不影响后续密文块的解密，若第t块密文块正确，则第t+1个明文块就能正确提出

      • CBC相关攻击手段拓展：https://www.cnblogs.com/p00mj/p/11797786.html

      • 特点：

        • 若加密时有一组明文发生错误，则后面的密文都受到影响，但是解密时只有该组不能正常解密，其余均能正常解密
        • 若解密时有一组密文发生错误，则只会影响该组和后面一组的解密结果

      • 报文的完整性认证：

        完整性认证的需求

        • 功能需求：能够检测数据被篡改

        • 安全需求：不同的消息有不同的摘要，从摘要无法恢复消息

        • 性能需求：算法简单易实现，摘要尽可能短

          首先根据明文分组生成奇偶校验码r的分组：

          然后利用CBC模式，对附带校验码的明文(m,r)加密，最后一个分组就是认证码

          若不想加密，仅想对明文认证，可以传送明文m和认证码

          若想加密和认证，传送密文C和认证码

          如何对认证码进行校验呢？重复计算一遍认证码

    • 密码反馈模式CFB：

      • 定义：若待加密消息需要按字符、字节或比特处理时，可采用CFB模式(比如数据库加密要求不能改变明文的字节长度的时候就需要以字节为单位进行加密)，CFB模式同样需要初始向量IV
      • 特点：
        • 相同明文：和CBC模式一样，改变IV同样导致加密结果不同
        • 链接依赖性：类似CBC，重排密文组会影响解密
        • 错误传播：一个或多个比特错误出现在任意一个r比特的密文组中会影响这个组和后继个分组
        • 错误恢复：类似CBC，也是自同步，但是需要个密文组才能还原

    • 输出反馈模式OFB：

      • 定义：结构类似CFB，但是反馈的内容是DES的输出而不是密文；其实说白了就是类似大一点的流密码，对着IV不断加密，加密一次就相当于获取了一个子密钥
      • 特点：
        • 相同明文：改变IV同样会导致加密结果不同
        • 链接依赖性：密钥流独立于明文
        • 错误传播：有一个或多个比特错误的任意密文字符仅仅会影响该字符的解密
        • 错误恢复：OFB模式能从密文比特错误中得以恢复，但在丢失密文比特后就无法实现自同步了，因为会破坏密钥流的编排

    • 计数器模式CRT：

      定义：可以看做是OFB模式的简化版本

      优点：

      • 效率高
      • 加密数据块的随机访问
      • 可证明安全
      • 简单

  • 不同工作模式的应用场景：

    • 什么时候用ECB？明文消息长度小于等于分组长度
    • 什么时候用CBC？一是消息认证的时候，二是明文不易丢信号且对格式没要求
    • 什么时候用CFB？一是对格式有要求，二是容易丢信号
    • 什么时候用OFB？一是信号很容易出错，二是不易丢信号

加密模式参考资料：

  • https://blog.csdn.net/weixin_42368982/article/details/125529969

  • https://l2x.gitbooks.io/understanding-cryptography/content/docs/chapter-2/cfb.html

3.8 有限域基础

  • 定义：

    加法和乘法都是群，且加法和乘法都是交换群的非空集合

  • 引理：

    对于任意素数p，为域，元素个数为p个

  • 域上的多项式环：

    加法和乘法都是模f(x)的运算

    注意：上面的多项式不一定有逆元

  • 引理：

    r(x)在模f(x)下有逆元，当且仅当r(x)与f(x)互素

  • 不可约多项式：

    若次数比f(x)低的多项式都与f(x)互素，则f(x)为不可约多项式

  • 对于任意首项系数为1的不可约多项式，F(x)/f(x)为域

  • 若，则F[x]/f(x)中元素个数为个

  • 域的构造方法：首先选取中的一个n次不可约多项式，然后构造集合

  • 域

    • AES加密是以字节为处理单元，可以将每一个字节看做是有限域上的一个元素，分别对应于一个次数不超过7的多项式

    • 还可以将每个字节表示为一个十六进制数，代表较高位的4bit的符号仍在左面

    • 函数xtime(x)：

      定义为GF(x)上的xb(x)：

      • 若，把字节b左移1位，在最右面补上0
      • 若，把字节b左移1位，在最右面补上0，再与1B异或

3.9 AES算法

  • AES密钥长度可变：128、192、256，可进行组合
  • AES采用SP结构，轮函数由3个不同的可逆均匀变换构成，称为3个层
    • 线性混合层：确保多轮之后的高度扩散
    • 非线性层：将具有最优的“最坏情况非线性特性”的S盒并行使用
    • 密钥加层：单轮子密钥简单的异或到中间状态上，实现一次性掩盖

AES规定：

  • 明文长度固定为128位
  • 密钥长度可以为128,192,256位，分别循环10,12,14轮

整体的加密过程：

  • 初始变换

    将明文与密钥按字节异或

  • 9轮循环运算

    1. 字节代换

      S盒：Sub-Box，让一个字节与另一个字节进行映射(这里与DES的S盒不同，并没有压缩数据)

      每一个明文的字节可以看做一个S盒中的x和y的坐标

    2. 行移位

      第一行不变，第二行左移1个字节，第三行左移2个字节，第四行左移3个字节

    3. 列混合

      也就是将输入的4*4矩阵左乘一个给定的4*4矩阵，这里的乘法不是普通意义上的乘法

    4. 轮密钥加

      将列混合后的字节矩阵与子秘钥矩阵进行异或

  • 1轮最终轮

    类似循环运算，但是没有列混合

graph LR
sub("初始变换(128bit，即4x4矩阵)")-->A
subgraph 9轮循环运算
D-->|9轮|A
A(1字节代换-S盒)-->B(2行移位)
B-->C(3列混合)
C-->D(4轮密钥加)
end
subgraph 最终轮
AA(字节代换)-->BB(行移位)
BB-->CC(轮密钥加)
end
D-->AA
CC-->G(密文)

密钥编排：

  • 定义：指的是从种子密钥得到轮密钥的过程由密钥拓展和轮密钥选取两部分组成

    轮密钥的比特数等于分组长度乘以(轮数+1)

  • 可以获得10/12/14轮的子密钥

  • 符号解释：

    • ：每一列有4字节的密钥，就是密钥列数

  • 过程：

    • 若：

      • 若不是整数：

      • 若是整数：

        函数T由3部分组成：

        • 字循环：左移一位
        • 字节代换：对字循环的结果利用S盒代换
        • 轮常量异或：将前面两步的结果与轮常量Rcon[j]异或，j表示轮数

    • 若：

      在上面的基础上多了一个判断：

      若，需要再进行一次字节代换

AES参考资料：

https://www.bilibili.com/video/BV1i341187fK

3.10 SM4算法

  • 概况：

    • 分组长度和密钥长度均为128bit
    • 加密和密钥拓展都采用32轮非线性迭代结构
    • 解密算法和加密算法结构相同，只是轮密钥的使用顺序相反

  • 术语：

    • 表示e比特的向量集，中的元素称为字节，中的元素称为字
    • S盒是一个固定的8bit输入和8bit输出的置换
    • 两个基本运算：
      • ：32bit异或
      • ：32bit左循环移i位

  • 加密算法：

    • 32轮迭代

      其中

      其中T为一个可逆变换，由非线性变换和线性变换L复合而成

    • 1次反序变换

      就是顺序反过来

  • 密钥编排：

    • 长度为128bit，记为

    • 轮密钥为，为32bit

    • 系统参数：，为字

    • 固定参数：，为字

    • 具体过程：

      • 首先计算K：

        然后计算：

        其中是在的基础上将线性变换变成：

四、公钥密码

4.1 公钥密码的基本概念

若采用对称密码体制来保护用户之间的通信：需要N(N-1)/2个密钥

对称密码体制有哪些缺点？

  • 密钥管理(用户数量非常大的时候)
  • 密钥分发，因为安全通信的前提是有一个共同的秘密信息
  • 不支持开放系统，若两个没有预先建立关系的用户需要建立安全通信，是没办法共享一个密钥的

Diffie和Hellman提出了公钥密码体制

公钥密码体制的基本思想：

  • 把密钥分为两部分，也就是公钥和私钥，公钥可以向外公布，私钥却是保密的。密钥中的任何有一个可以用来加密，另一个用来解密。已知密码算法和密钥中的一个，求解另一个在计算上是不可行的。

4.2 完全剩余系

等价关系：满足自反，对称，传递

整数的同余关系是一个等价关系，按照同余，全体整数可按照是否模m同余划分若干个两两不相交的集合，每一个这样的集合称为模m的同余类或剩余类

定理一：

  • 对于给定的正整数m，有且恰有m个不同的剩余类，模m的m个剩余类可分别记为[0],[1]...[m-1]，括号中的数为余数

完全剩余系：

  • 在模m的所有剩余类中各取一个代表元，a1,a2...am为一个完全剩余系

最小非负完全剩余系：

  • 0,1,2,3...m-1
  • 通常情况下，表示模m的最小非负完全剩余系集合，中的加法减法乘法都是模m下的运算

定理二：

  • 设m为正整数，gcd(a,m)=1,则若x遍历m的一个完全剩余系，ax+b也遍历m的一个完全剩余系

定理三：

  • 设为正整数，且，x遍历的完全剩余系，y遍历的完全剩余系，则遍历的一个完全剩余系

4.3 简化剩余系

在模m的一个剩余类中，若一个数与m互素，则该等价类与m互素

定义一：

  • 对于任意一个素数m，

定义二：

  • 在模m的个与m互素的剩余类中，每一个挑选一个代表元，则组成的集合为简化剩余系或者说既约剩余系
  • 中与m互素的数构成的集合称为最小非负既约剩余系
剩余系

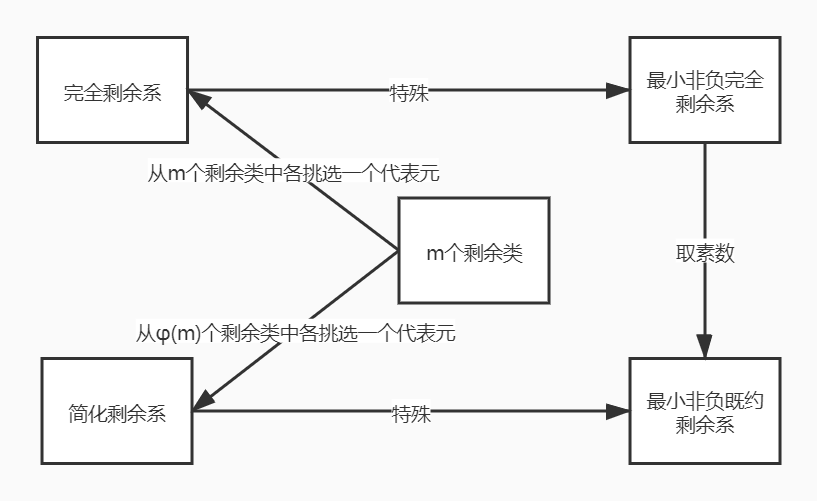
定理一：

  • 设m为正整数，gcd(a,m)=1,则若x遍历m的一个简化剩余系，ax也遍历m的一个简化剩余系

定理二：

  • 设为正整数，且，x遍历的简化剩余系，y遍历的简化剩余系，则遍历的一个简化剩余系

4.4 欧拉定理

推论一：

  • 设gcd(m,n)=1，则

定理一：

  • 若，则

定理二(欧拉定理)：

  • 设r为模m的最小非负简化剩余系中的一个元素，则

4.5 RSA加密算法

密钥生成：

  • 选择两个大素数p，q
  • 计算n = pq，z = (p-1)(q-1)
  • 选取
  • 选取d，使得
  • 公钥：(e,n)，私钥：(d,n)

加密：

  • 注意：m<n

4.6 群的概念

概念：

  • 设G是一个具有代数运算的非空集合，且满足以下三个条件，则称之为群
    • 封闭性
    • 结合律
    • 有单位元
    • 有逆元

常见群：

  • (整数，加法)：整数加群
  • (模n的最小非负完全剩余系，加法)
  • (全体非零实数R*，乘法)
  • (全体正实数R+，乘法)

阶：

  • 有限群的元素个数，记为

有限群的判定：

  • 定理一：
    • 一个有限集合G，若乘法满足封闭性，结合律，消去律，则G是群
    • 例子：m的最小非负简化剩余系，对于乘法是一个群

4.7 循环群

定义：

  • 设G为一个群，若存在一个元素a，使得G=<a>，则G为循环群，a为生成元，若，则成为无限循环群，否则成为有限循环群

  • 例子：

    • m的最小非负简化剩余系是循环群
    • 整数加法群Z是循环群，生成元为1或-1
    • 模m的剩余类加群为循环群，生成元为[1]

  • 群中的离散对数问题

    • 设G=<a>为循环群，给定G中一个元素h，找到正整数k，使得，我们把k成为h相对于生成元的离散对数

    • 对于整数加群，离散对数问题是平凡的，那么在什么群里面不平凡呢？

      在中，离散对数问题难以解决

4.8 ElGamal加密

密钥生成：

  • 选取一个较大的素数p
  • 选取生成元g
  • 选取
  • 公钥私钥

加密：

  • 其中

解密：

与RSA的区别：

  • 数学困难问题
  • 公开参数设置

4.9 椭圆曲线的基本概念

  • 椭圆曲线的表示形式：，，记为E(a,b)，简记为E

  • 加法的几何描述：若E上的3个点位于同一直线上，那么他们的和为O，从此可以确认加法规则

    • O为单位元，对于E上的任何一点P，有P+O=P

    • 设P和Q的x坐标不同，定义P+Q如下：作直线l经过P和Q交E于R，过R作直线l'平行于y轴，则l'与E的另一点S为P+Q。

    • 当P和Q的x坐标相同，则Q=-P，用一条处置的线连接这两个点，可看做是在无穷远点和椭圆曲线相交，P+Q=O

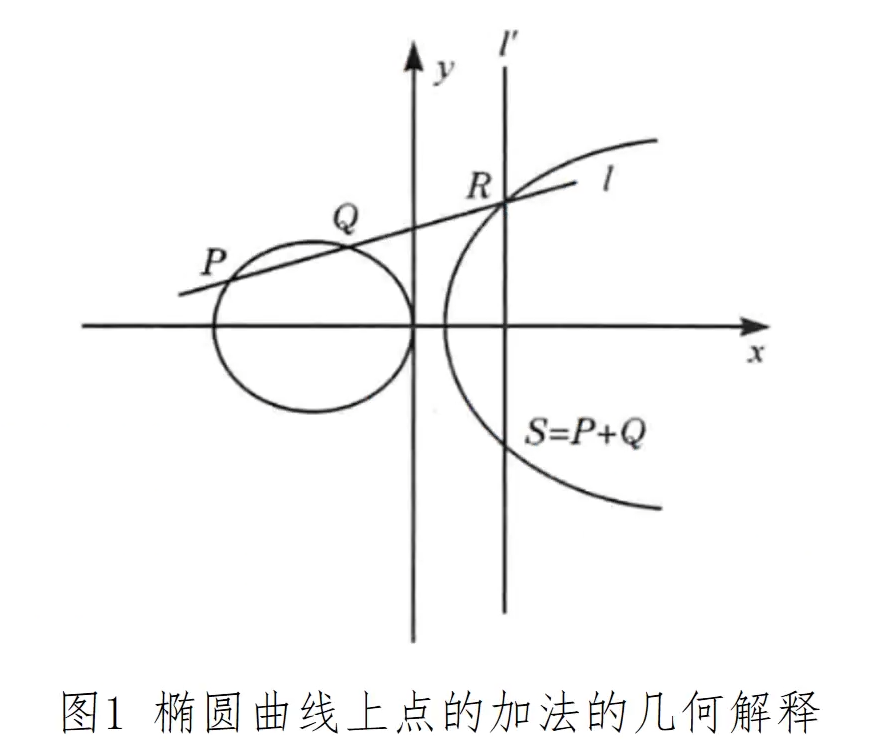
      image-20230508191209908

  • 加法的代数描述：

    • 设，定义

      其中

4.10 椭圆曲线密码学

阶：已知点P，求n满足nP=O，n称为P的阶

椭圆曲线上的离散对数问题：

  • 已知曲线上：Q=mP，求解m的问题

加解密：将明文m编码为E上的一个点，然后对该点做加密变换

  • 密钥生成：在曲线上选取基点P，同时选取大数k为私钥
  • 加密：
  • 解密：

ECC参考资料：

https://www.bilibili.com/video/BV1v44y1b7Fd?t=1461.8

4.11 SM2

符号：

  • ：上椭圆曲线E的所有有理点(包括无穷远点)组成的集合
  • ：包含q个元素的有限域
  • G：椭圆曲线的基点，其阶为素数
  • ：消息摘要长度为v比特的密码杂凑函数
  • KDF：密钥派生函数
  • M：待加密的消息
  • M'：解密后的消息
  • n：基点G的阶
  • ：用户B的公钥
  • q：有限域中元素的个数

SM2算法参数：

  • p：的特征p，为m比特长的素数p，通常为160比特
  • SEED：长度不小于192比特的比特串
  • a，b：椭圆曲线参数，为上的两个元素
  • G：基点
  • n：G的阶
  • h：余因子，为曲线的点数

密钥产生：

  • 私钥：
  • 公钥：

五、Hash函数

5.1 Hash概念和基本要求

定义：

  • 将任意长的消息M映射为较短的固定长度的一个值H(M)，又称散列函数，压缩函数，杂凑函数，指纹函数等，其值为哈希值，散列值，杂凑码，指纹，消息摘要等

哈希函数应该满足的条件/特点？

  • Hash函数的输入可以是任意长
  • Hash函数的输出是固定长
  • 易于在软件和硬件中实现
  • 输入无法推导出输出，当输入变化时，输出不可预测

Hash函数为了实现安全认证，需要满足如下安全条件：

  • 单向性

  • 抗弱碰撞性：已知x，无法找到y使Hash相同

  • 抗强碰撞性：找任意x，y，使其Hash值相同也是不可行的

    任何一个Hash函数，若满足抗强碰撞性，则一定满足抗弱碰撞性，则一定满足单向性(反证法)

5.2 生日攻击

第一类生日攻击：

  • H(x)有n个可能的输出，若随机选取k个输入，至少有一个y使得H(y)=H(x)的概率为0.5，则k有多大？对于寻找上述y的攻击为第一类生日攻击
  • 产生特定输出的概率是1/n，故的概率为,故随机取k个随机值得到的输出中都不为H(x)的概率为，则至少有一个等于的概率为，约为，故若概率为0.5，且H的输出为m比特长，则

第二类生日攻击：

  • 设有k个整数项，每一项都在在1和n之间等可能的取值，P(n,k)：k个整数项中至少有两个取值相同的概论
  • ，令P>0.5，得，在Hash函数中，

这种生日攻击给出了消息摘要长度的下界，一个40bit的消息摘要是十分不安全的

5.2 SHA-1算法

  • 算法的输入：小于的比特长的任意消息，分为512比特长的分组

  • 算法的输出：160比特长的消息摘要

  • 算法处理步骤：

    1. 填充：首先补一个1，然后补充0，直到满足，也就是剩下64位，存储消息长度

    2. 附加消息的长度：留出的64bit存放消息被填充前的长度，若大于则取模，采用大端模式

    3. 对MD缓冲区初始化，缓冲区为5个32bit以大端方式存储数据的寄存器A,B,C,D,E，下面为初始值

    4. 以分组为单位对消息进行处理

      每一分组都经过一压缩函数处理，压缩函数由4轮处理过程组成，每一轮又由20步迭代组成

      第四轮的输出(也就是第80步迭代输出)再与第一轮的输入(也就是ABCDE)相加，产生(也就是新的ABCDE)，其中加法是缓冲区5个字中的每一个字与中相应的字模相加

    5. 输出消息

  • 压缩函数：

    • 每一轮迭代：

      • t：迭代次数
      • ：基本逻辑函数
      • CLS：循环左移
      • Wt：由当前512比特长的分组导出的一个32比特长的字
      • Kt：加法常量
      • +：模的加法

    • 基本逻辑函数：

      迭代步数 函数名 定义

    • Wt的产生：

      将512bti分为16份*32bit的小分组，记为M[i]

    • 常量字Kt：

  • 总结：

    SHA-1可以大体上分为两部分，第一部分是填充和分组，第二部分是80轮迭代；对于第一部分，首先是填充然后加上填充前的长度，然后按照512一组进行分组；对于第二部分，同样可以分为3个小部分，第一部分是初始化ABCDE和对16份*32bit的数据进行填充，第二部分是进行80轮迭代，第三部分是与原始的ABCDE进行相加

  • 参考资料：https://www.bilibili.com/video/BV1Ua411679P?t=903.1

5.4 SM3算法

定义：

  • SM3是中国国家密码管理局颁布的中国商用密码标准算法

与SHA-1的不同：

  • 个人感觉，和SHA1很像，比如也是可以分为两个部分，第一部分是填充和分组，第二部分是迭代，第一部分一模一样，第二部分也是首先进行数据扩充，在SHA1中，由16份32bit数据扩充成80份，在SM3中，扩充成了68份数据和64份数据，然后在压缩函数中进行压缩，最后与寄存器初始值进行异或，成为下一组数据的输入，主要的不同就在压缩函数

数据扩充：

  • 对于j从16到67：
  • 对于j从0到63：

压缩函数：

  • 符号说明：

    • ：第i个消息分组

    • CF：压缩函数

    • ：布尔函数，随j的变化取不同的表达式

    • ：布尔函数，随j的变化取不同的表达式

    • ：压缩函数中的置换函数，

    • ：消息扩展中的置换函数，

    • ：算法常量

  • 具体过程

    对于j从0到63：

    然后：

  • 参考资料：https://www.bilibili.com/video/BV1gi4y1C7zf?t=1286.1

六、数字签名

6.1 数字签名的基本概念

数字签名必须保证：

  • 接收者能够核实发送者
  • 发送者不能否认
  • 不能伪造

算法组成：

  • 密钥生成
  • 签名算法
  • 验证算法

6.2 RSA签名算法

过程：

  • 就是RSA加密的另一种形式，只不过传统加密是用公钥加密，这里是用私钥加密

缺点：

  • 存在唯密钥攻击下的存在性伪造(参考：https://www.bilibili.com/video/BV1Nv4y1a7ib?t=465.2)
  • 速度慢。因为需签名的消息，所以每次只能对位长的数据进行加密

补救办法：

  • 添加Hash函数

6.3 ElGamal签名算法

签名过程：

  • 已知公钥，私钥

  • 随机取，计算：

验证过程：

  • 计算

为什么s是模p-1？减小计算量

  • 费马小定理：$a^pa mod p ，其中为素数；当不是的倍数：a^{p-1} mod p$
  • ，可减少计算量

为什么s不是模p？可能结果不对

  • ，当n≠0，

参考：https://www.zhihu.com/question/438123526

6.4 DSA签名算法

密钥生成：

  • 全局公开钥：

    • p：选取素数，其中，且L是64的倍数

    • q：，且q是p-1是素因子

    • g：随机选取整数h，其中，且

  • 用户私钥：

    • x：随机选取整数x，，计算

  • 用户公钥：y

签名算法：

  • 对于消息m，随机选取一个整数k，，然后

验证算法：

  • 计算

    验证等式

    若等式成立，则签名有效，否则无效

参考资料：DSS数字签名标准 - mengsuenyan - 博客园 (cnblogs.com)

6.5 其他签名算法

6.5.1 Schnorr签名体制

公开参数：

  • p：
  • q：，且是p-1的素因子
  • g：，且

用户私钥：

  • x：

用户公钥：

  • y：

签名过程：

  • 选取随机数，计算
  • 计算
  • 计算
  • 得到数字签名(e,s)

验证过程：

  • 计算
  • 验证

6.5.2 Okamoto签名体制

公开参数：

  • p：
  • q：，且是p-1的素因子
  • ：两个与q同长的随机数

用户私钥：

  • ：两个小于q的随机数

用户公钥：

  • y：

签名过程：

  • 选取两个小于q的随机数
  • 计算哈希：
  • 计算
  • 计算
  • 得到数字签名

验证过程：

  • 计算
  • 计算
  • 验证

6.6 特殊性质的签名算法

  • 盲签名：

    就是A让B签署文档，但是A不向B泄露任何关于文档内容的技术

    特性：

    1. 消息的内容对于签名者是不可见的
    2. 签名泄露后，签名者不能追踪签名

    应用：

    • 选举协议，安全电子支付系统

    过程：

    • 随机选择，计算

  • 群签名：

    可以隐藏签名者的身份，宏观上是一群人一起签名

    一旦出现争端，可借助群成员或一个可信机构识别出签名者

  • 不可否认签名：

    • 组成：

      • 签名算法

      • 验证协议

      • 否认算法

  • 代理签名

七、密码协议

7.1 Diffie-Hellman密钥交换

交换过程：

  • 协商一个素数p以及素数的本原元g
  • 用户A选择随机数x<p，计算
  • 用户B选择随机数y<p，计算
  • 二者相互交换和
  • 计算密钥

安全性：

  • 不可破获密钥，因为是基于离散对数问题
  • 容易受到堵塞攻击：攻击者发起大量密钥请求，耗尽主机计算资源
  • 容易遭受中间人攻击

ECDH：ECC和DH的结合

设

Bob：

Alice：

Bob将Q1传递给Alice，Alice将Q2传递给Bob

然后对于Bob：

对于Alice：

此时二者的私钥相同，Q充当了私钥的角色

7.2 Shamir秘密分享

门限方案的定义：

  • 秘密s被分为n个部分，每个部分称为份额或者影子。由k个或者多于k个参与者所持有的部分信息可重构s，少于k个则不行，则称该方案为(k,n)秘密分割门限方案，k称为门限值。少于k个参与者所持有的的部分信息得不到s的任何信息称该方案是完善的

门限方案的算法组成：

  • 份额分配算法
  • 恢复算法

构造思路：

  • 设平面上有k个不同的点，则存在唯一的k-1次多项式通过这k个点。若把秘密s取做f(0)，n个份额取做f(i)，那么利用其中任意k个份额就可以重构f(x)，从而得到秘密s

  • Shamir门限方案：

    • 设GF(q)为大素数q生成的有限域，其中

    • 秘密s是GF(q)/{0}上均匀选取的随机数

    • 在GF(q)上构造一个k-1次多项式

      其中

    • n个参与者，其中的份额为，任意k个参与者要得到秘密s，需要解方程

    • 由拉格朗日公式：

      故

7.3 Kerberos认证

Kerberos设计目标：

  • 安全性：有效防止攻击者假扮成另一个合法的授权用户
  • 可靠性：分布式服务器架构，提供相互备份
  • 对用户透明性
  • 可伸缩：能够支持大数量的客户和服务器

Kerberos解决的问题：

  • 口令明文传送/次数太多
    • 引入票据许可服务器TGS，进行票据重用
    • 用户和AS之间共享密钥
  • 票据的有效性(多次使用)
    • 引入时间戳和有效期机制
  • 访问多个服务器则需要多次申请票据(口令多次使用)

Kerberos(V4)的缺陷：

  • 依赖性：依赖于DES和IP协议
  • 票据有效期：最小5分钟，最大21小时
  • 认证转发能力：不允许签发给一个用户的鉴别证书转发给其他工作站
  • 领域间的鉴别：管理起来困难
  • 加密操作缺陷：非标准形式的DES加密，易受攻击
  • 会话密钥：存在着攻击者重放会话报文的可能
  • 口令攻击：未对口令提供额外的保护

八、可证明安全

8.1 Boneh-Franklin身份基加密算法

PKI公钥密码体制的问题：

  • 发送者必须拥有接收者的证书
  • 证书管理和CRL的复杂性
  • 证书数据库被暴露给组织/机构

身份基公钥密码体制的优势：

  • 针对未准备用户的密码学
  • 公钥不再不可读，是用户身份的某些属性，比如电子邮件地址
  • 发件者只需要知道接收者的身份属性即可发送加密邮件，在根本上解决了认证问题
  • 接收者在收到加密邮件之后才需要与系统交互

九、信安数学补充

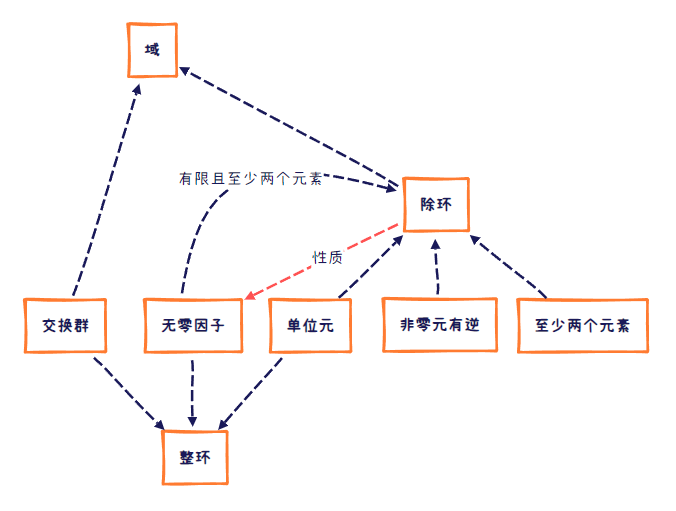
9.1 群环域

群到环再到域其实是一个范围不断变小的过程。这一部分比较抽象，需要记忆的性质也比较多，我认为可以对其进行分层记忆。首先群这方面的定义可以分为五层：

  • 封闭性
  • 结合律
  • 单位元
  • 逆元
  • 交换律

对于一般的群，满足上面四层就足够了，层数越往上也就越基础。

为了方便理解，我愿称交换群也就是阿贝尔群为满级群。

从群到环，也就是满级群上升了一个新台阶，引入了另一种运算，乘法。

环的定义比较复杂，但是我们依然可以分层进行学习：

  • 封闭性

  • 结合律

  • 单位元

  • 逆元

  • 交换律

  • 分配律

  • 无零因子

对于最原始的环，除了对于加法的五个要求外，对于乘法，只需满足最基础的封闭、结合律还有对于加法的分配律

在原始环的基础上，若再修炼一个有单位元，便是有单位元环；若仅仅修炼一个交换律，便是交换环

那么什么是整环呢？就是在既是有单位元环，又是交换环，还得再加一个无零因子

除环我认为可以是差一步到域，因为在除环中，去掉0后，剩下的元素已经满足一个乘法群了，若乘法群可交换，则成为域

image-20230518232923313
Courses
#现代密码学 #计算机基础知识
现代密码学
https://d4wnnn.github.io/2023/04/07/Courses/现代密码学/
作者
D4wn
发布于
2023年4月7日
许可协议