GFSR与TGFSR

GFSR

首先介绍一下 Kendall 随机数生成算法。

设序列 生成方法如下：

并且基于本原多项式

例如，，

则得到序列

可以看到序列的下标是从 0 到 30，也就是有 31 个元素。设每 5 个元素一组，得到如下的 Kendall 序列 (注意顺序是从右到左，例如 ，则序列中是 )。

上面的 Kendall sequence 的周期是由 Word 字大小确定的，而每个周期内的 Word 顺序也是不变的。

而 GFSR 在此基础上进行了改改进。

本原多项式仍为 , 设序列 被划分为 列，其中 。在列与列之间设置一个平移参数 。

还是以上面的 为例。

观察上面的 Fig.4，竖着看，第一列就是 的 31 个元素。而第二列与第一列相比，"平移"了 6 个元素，第 3 列等以此类推。

我们可以看到，每一列遵循：

因而每一行 (一个 Word)也必须遵循：

def gfsr1():  
    iv = [  
        [1, 1, 0, 1, 0],  
        [1, 0, 0, 0, 1],  
        [1, 1, 0, 1, 1],  
        [1, 1, 1, 0, 0],  
        [1, 0, 0, 1, 1]  
    ]  
    for i in range(5):  
        print(i, iv[i])  
    for i in range(5, 32):  
        x = []  
        for j in range(5):  
            x.append(iv[i - 3][j] ^ iv[i - 5][j])  
        print(i, x)  
        iv.append(x)

|276

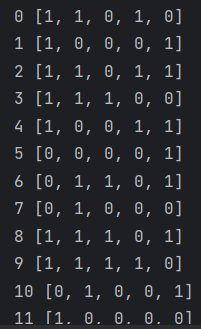
我们可以看到，每一个 Word 都出现了一次而且仅仅一次。

是不是设置任意的 效果都相同？答案是否定的。我们可以根据 starting matrix，即 来验证。

还是以刚才的本原多项式为例。

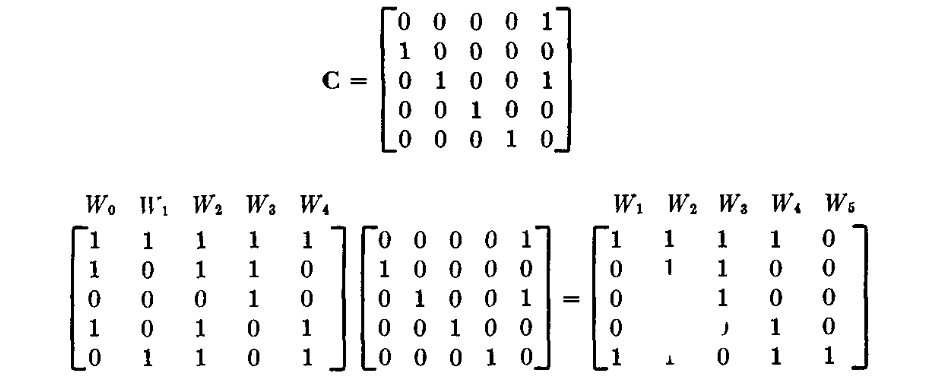
根据上图，我们可以看到 。经过 31 次运算后，。而每一次运算都能得到新的 Word，只需要 线性无关即可。

由于上图可以看到，在刚才的例子中，足足有 9999360 个这样的初始化语句。

进而，GFSR 的算法如下：

def gfsr2():  
    p = 5  
    q = 2  
    iv = [  
        [1, 1, 0, 1, 0],  
        [1, 0, 0, 0, 1],  
        [1, 1, 0, 1, 1],  
        [1, 1, 1, 0, 0],  
        [1, 0, 0, 1, 1]  
    ]  
    l = 0  
    for i in range(31):  
        print(i, iv[l])  
        for m in range(5):  
            iv[l][m] = iv[(l + q) % p][m] ^ iv[l][m]  
        l = (l + 1) % p

其实函数 gfsr2() 与 gfsr1() 相比只是优化了空间。

TGFSR

扭曲广义反馈移位寄存器 (Twisted Generalized Feedback Shift Register, TGFSR。

GFSR 是一种广泛使用的基于线性递归方程的伪随机数生成器，但是也有很多不足：

• 初始种子的选择在随机性中是非常关键和有影响的，并且良好的初始化相当复杂和耗时。
• GFSR 序列的每个比特可以被视为基于三项 的 m 序列，已知其具有较差的随机性。
• GFSR 序列 的周期远小于理论上限 。
• 该算法需要 n 个字的工作区域，如果同时实现大量生成器，这将消耗内存。

但是 TGFSR 相比 GFSR 的改动只有一点，就可解决上面的缺点。

即，将

换成

其中 是一个 的矩阵。

具体来说，如果只看最终的效果，改进如下：

即将 换成 。其中 代表右移， 代表最低有效位。