Linux随机数生成机制

随机数生成器是几乎所有密码系统的关键模块，Linux 作为最受欢迎的开源系统之一，在内核中也提供了伪随机数生成算法，Linux pseudo-random number generator(LRNG)，下面将对 LRNG 的算法进行介绍。

本文章主要参考了论文《Analysis of the linux random number generator》，并以论文中的 Linux 内核 2.6.10 版本为样例。

LRNG 的两个 API

在 Linux 中提供了两个 API 用于生成随机数，他们都是基于一个信息熵池生成随机数。信息熵池可以理解为一个包含了各种随机信息的集合，例如键盘的敲击按键，鼠标的移动等等。

• /dev/random：当信息熵池中的信息不足以生成随机数时，会阻塞直到熵池中的信息数目能够满足要求。
• /dev/urandom：不会阻塞请求。

在 Linux 中，我们可以通过如下的命令调用 /dev/random 生成随机数。

head /dev/urandom | md5sum | head -c 20

LRNG 的结构

LRNG 的结构可以分为 3 部分：

• 将系统事件转换为熵
• 将熵添加到熵池
• 通过 3 个连续的 SHA-1 操作来生成生成器的输出和输入到池中的反馈

每一个系统事件都可以表示成两部分：

• 事件产生的时间
• 事件值 (例如按键的编码)

为了跟踪添加到池中的物理随机性的数量，LRNG 持有一个计数器，该计数器计算为不同事件频率的函数，后面会详细介绍。

生成器结构

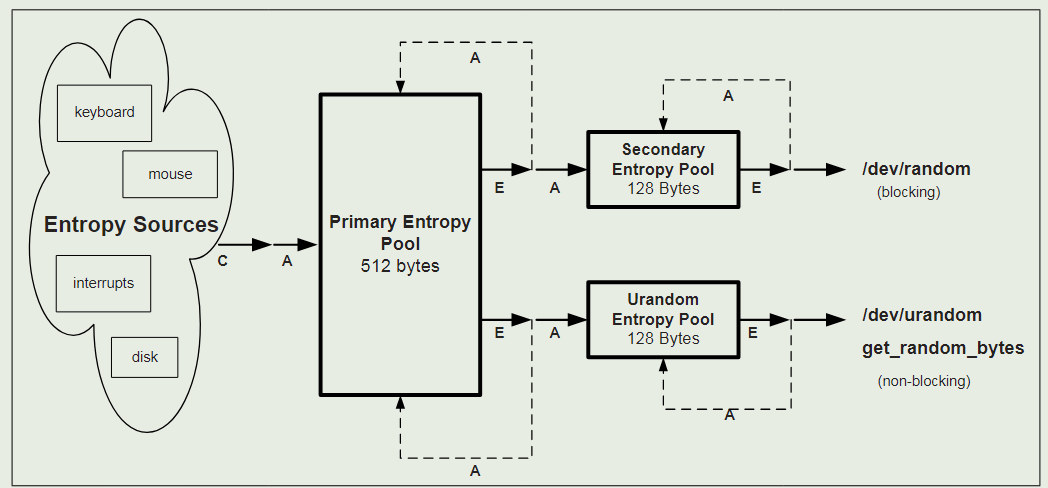
熵池

如图，LRNG 内部有 3 个熵池：

• Primary Entropy Pool，512 字节，128word，熵池 1
• Secondary Entropy Pool，128 字节，32word，熵池 2
• Urandom Entropy Pool ，128 字节，32word，熵池 3

熵源将数据添加到熵池 1 中，从熵池 1 中提取输出并输入到熵池 2 和熵池 3 中。

添加物理熵

物理熵有 4 个来源：

• 鼠标
• 键盘
• I/O 活动
• 中断

当上面的事件发生时，生成一个 32bit 的时间和 32bit 的属性值(如按键的编码)。

输出

• /dev/random 调用熵池 2
• /dev/urandom 调用熵池 3
• 当熵池 2 和熵池 3 的熵不够时调用熵池 1

初始化

操作系统在开机时，会进行常规检查，这些步骤都是类似的，因此攻击者很可能会成功预测。即使加上时间戳，攻击者也可以在有限的次数内成功爆破。因此，我们需要对熵池进行初始化而不是从空熵池开始。

当操作系统关机时，会调用 /dev/urandom 读取 512 字节的数据并且存储到文件中。当系统开机时，读取此种子文件，写入到 /dev/urandom。而 /dev/urandom 被设置为当遇到写入的数据时，会转而写入到熵池 1。而熵池 2 和熵池 3 可以从熵池 1 中拉取数据，进而 3 个熵池全部得到更新。

估计熵量

前面我们提到，当调用 /dev/random 时，若熵量不足则阻塞。那么熵量是如何估计的呢？

设 为事件 的时间，则：

熵量通过上面的 3 个值进行计算：

也就是说，外部事件添加的熵量是根据如上的公式计算的，而这与香农定义的熵并不相同，注意区分。

当从熵池中提取 n 比特随机数时，熵池也进行更新 (在下面的章节将详细阐述)，熵量也减去 n。

而当熵池 A 向熵池 B 转移 m 比特的随机数时，熵池 A 的熵量减去 m 而熵池 B 的熵量加上 m。

当用户向 /dev/random 或者 /dev/urandom 写入数据时，熵量不变。

更新熵池

更新熵池基于 TGFSR。

对于熵池 1：

对于熵池 2 和熵池 3：

我们首先来看熵池 2 和熵池 3 是如何更新的。前面我们提到，这两个熵池的长度都是 128 字节，而在 32bit 的 PC 中，一个 word 是 32 bit，4 字节，因此这两个熵池都是 32 个 word 的长度。

假设我们要更新的熵池为 pool，要更新第 j 个 word，更新的熵 g 为一个 word 大小。

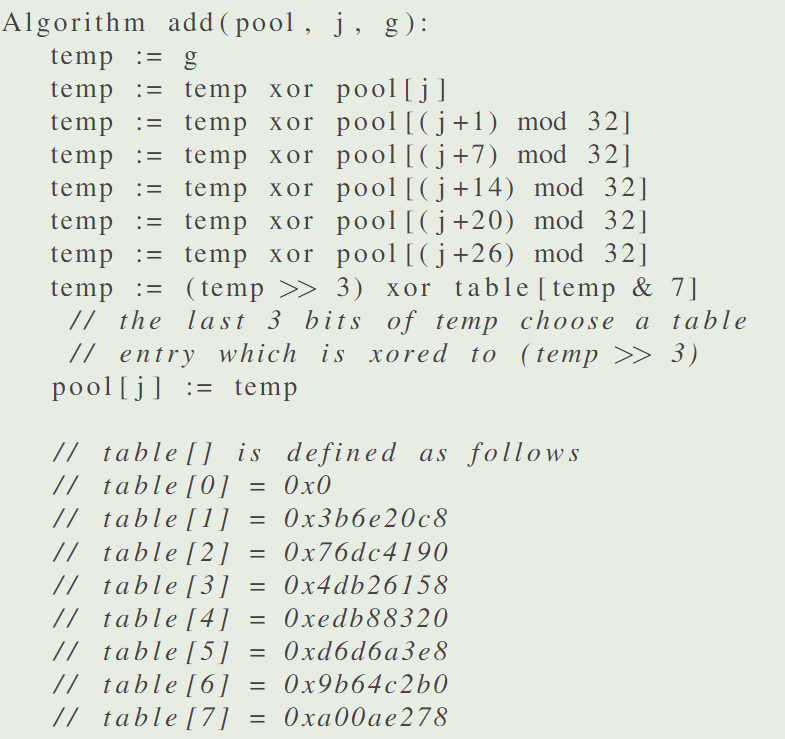
提取熵信息

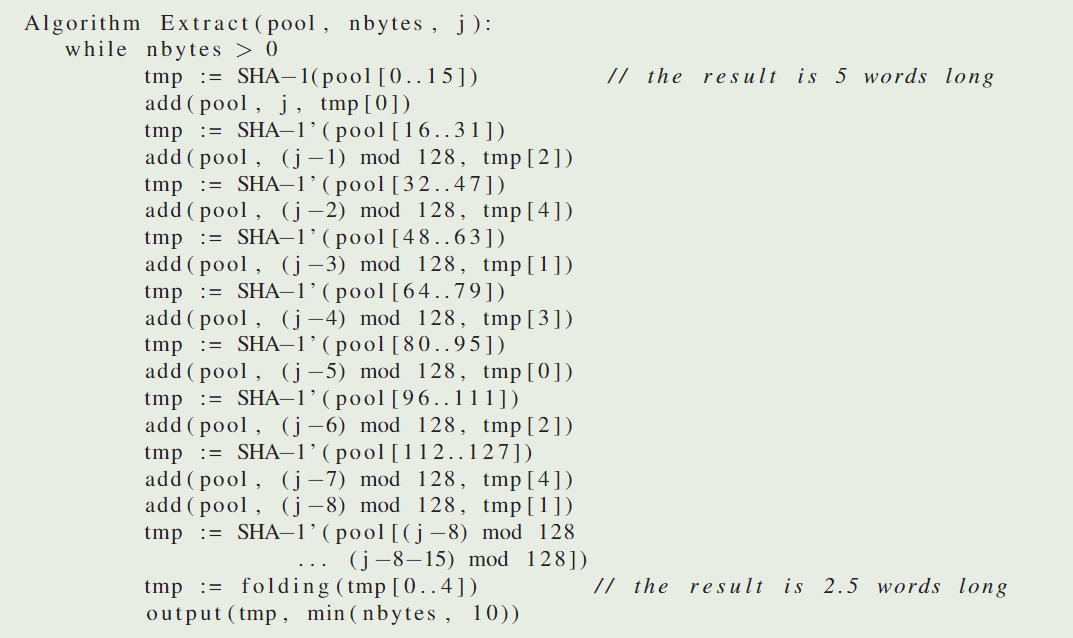
现在有 3 个熵池，假如我们最终要提取 10 字节作为随机数，我们该如何操作？

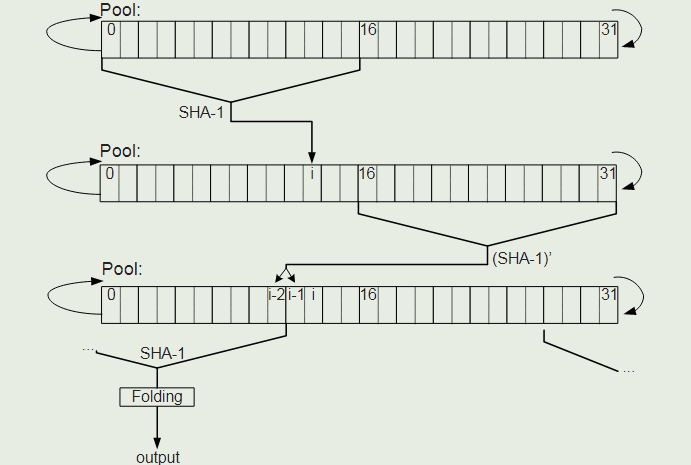
如图：

1. 首先，我们对前 16 个 word 执行 SHA-1 操作，然后将熵池的位置 i 设置为结果的一部分。
2. 然后对后 16 个 word 执行 SHA-1' 操作，然后将熵池的 i-1 和 i-2 位置设置为结果的一部分。
3. 最后对以位置 i-2 为结尾的 16 个 word 再次执行 SHA-1' 操作，得到了 20 字节。

在得到 20 字节的随机数后，我们使用如下的方法将其压缩成 10 字节：

熵池 2 和熵池 3 提取的代码如下：

|500

熵池 1 提取的代码如下：

参考资料

Gutterman, Zvi, Benny Pinkas, and Tzachy Reinman. "Analysis of the linux random number generator." 2006 IEEE Symposium on Security and Privacy (S&P'06). IEEE, 2006.